- 線形計画問題
- 主問題:
min 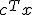
s.t. 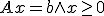
- 双対問題:
max 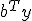 s.t.
s.t. 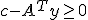
- ただし、Aの各行は1次独立で、許容領域は有界であることを仮定する。
- 単体法
- Aの列を選んで、正則な部分行列
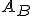 を作る。
を作る。
それ以外の部分を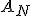 とする。
とする。
一般性を失わずに、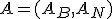 とできる。
とできる。
等式制約条件、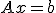 は、
は、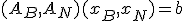 と書ける、
と書ける、
この条件の任意の解は、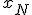 をパラメタとして、
をパラメタとして、
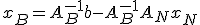 と置いて、
と置いて、
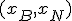 と書ける。
と書ける。
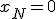 と取ったものは基底解、許容解になっている基底解を許容基底解と呼ぶ。
と取ったものは基底解、許容解になっている基底解を許容基底解と呼ぶ。
最適解は許容基底解のいずれかとなる。
単体法は、許容基底解を次々と辿って最適解となっている許容基底解を探す方法。
- 非退化仮定
任意の主問題の許容基底解が、0を要素に持たないことを仮定する。
- 非退化仮定から、許容基底解から
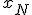 を微小に動かしても許容解となる。
を微小に動かしても許容解となる。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
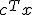
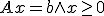
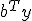 s.t.
s.t. 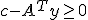
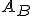 を作る。
を作る。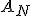 とする。
とする。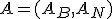 とできる。
とできる。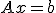 は、
は、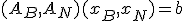 と書ける、
と書ける、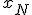 をパラメタとして、
をパラメタとして、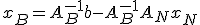 と置いて、
と置いて、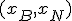 と書ける。
と書ける。
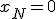 と取ったものは基底解、許容解になっている基底解を許容基底解と呼ぶ。
と取ったものは基底解、許容解になっている基底解を許容基底解と呼ぶ。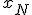 を微小に動かしても許容解となる。
を微小に動かしても許容解となる。