講義日程-2007年度冬学期
数理手法Ⅱ †
- 担当:河村 哲也 非常勤講師(お茶の水女子大学教授)
- 1.5単位
- 物工:限定選択
- 数理:限定選択B
- システム:限定選択※
- 16:30-18:00 工学部六号館 63講義室
- 教科書
内容 †
- 偏微分方程式の数値解法とその応用
- 大部分の偏微分方程式は解析的には解けない→数値的に解く。
- 物理法則に現れる偏微分方程式の多くは2階。
線形なものの方が解きやすい。非線形なものはできる範囲で線形化。
- 数理物理学に現れる偏微分方程式(PDE,Partial Differential Equation)
⇔常微分方程式(ODE,Ordinal Differential Equation)
- 二つ以上の独立変数に対する偏微分を含んだ方程式。
- ラグランジュの偏微分方程式
u = u(x,y) は未知
P,Q,Rは既知として、
P(x,y,u)∂u/∂x + Q(x,y,u)∂u/∂y = R(x,y,u)~~について、~~補助方程式、dx/P = dy/Q = du/R という連立一階常微分方程式を解き、その解~~f(x,y,z) = a~~g(x,y,u) = b を使って、~~元の方程式の一般解は、任意関数φを使ってφ(f,g) = 0となる。
- ∂u/∂x + c∂u/∂t = 0 を解く。~~dx = dt/c ∧ du = 0 ⇒ u = a ∧ t-cx=bなので、一般解は~~φ(u,t-cx)=0~~uについて解けば u = ψ(t-cx)~~x軸正の方向へ速度1/cで平行移動している。
- 一次元波動方程式~~{(∂/∂t)^2-(k∂/∂x)^2}u = 0~~微分演算を因数分解。(∂/∂t-k∂/∂x)(∂/∂t-k∂/∂x)u = 0~~ξ=x-kt, η=x+kt と変数変換すると、~~(∂/∂ξ)(∂/∂η) u = 0⇒φ(ξ) + ψ(η)が一般解。
- 二次元ラプラス方程式~~{(∂/∂x)^2 + (∂/∂y)^2}u = 0 の解は正則関数か、複素共役が正則な関数。
- 物理現象からの導出
- 弦の微小振動。弦を微小区間に分割して運動方程式を立て、弦の曲がりが小さいとして一時近似。
- 二階の準線形偏微分方程式の分類
- 拡散方程式。熱伝導方程式。熱流は等温面に垂直に、温度勾配に比例して流れると見なす。~~ある領域Ω内部の熱量変化は、(∂/∂t)∫[Ω]TdV に比例。~~領域表面からの流入量は、温度勾配の面素方向成分に比例すると考えると、∫[∂Ω]gradT dS に比例。~~この二つが比例すると見なすと、(∂/∂t)∫[Ω]TdV = a^2∫[∂Ω]gradTdS = a^2∫[Ω]ΔTdV~~これが任意の領域で成り立つので、∂T/∂t = a^2 ΔT~~比例定数a^2は、質量密度ρ、比熱c、熱伝導率κを使って a^2=κ/(ρc) と書ける。
- ポアソン方程式~~熱源ありの熱伝導方程式の平衡状態の解。~~Δu = -f~~熱源なしの場合はラプラス方程式Δu = 0
- 波動方程式、{(∂/∂t)^2 - Δ}u = 0
- 二階の準線形偏微分方程式:二階の偏微分方程式で、ニ階偏微分について一次の方程式。
- 2変数の準線形偏微分方程式、A∂[x]^2 u + B∂[x]∂[y]u + C∂[y]^2 u = Dについて、~~ξ = ξ(x,y)~~η=η(x,y)と変数変換すると、~~a = A(∂[x]ξ)^2 + B(∂[x]ξ)(∂[y]ξ) + C(∂[y]ξ)^2~~c = A(∂[x]η)^2 + B(∂[x]η)(∂[y]η) + C(∂[y]η)^2~~b = 2A(∂[x]ξ)(∂[y]η) + B{(∂[x]ξ)(∂[y]η)+(∂[y]ξ)(∂[x]η)} + 2C(∂[y]ξ)(∂[x]η)~~として、a∂[ξ]^2 u + b∂[ξ]∂[η]u + c∂[η]^2 u = dという形に変換される。~~うまくξとηを選べば、a,bを0にすることができる場合がある。~~B-4AC>0のとき、双曲型。a=c=0となるように選べる。∂[ξ]∂[η]u = fの形、もしくは(∂[ξ]^2-∂[η]^2)u = fの形にまで簡単にできる。~~B-4AC=0のとき、放物型。∂[ξ]^2 u = fの形にまで簡単にできる。~~B-4AC<0のとき、楕円型。∂[ξ]∂[ξ^*]u = fもしくは(∂[ξ]^2+∂[η]^2)u = f の形にまで簡単にできる。~~標準化した式は、いずれも右辺には一階微分までしか含まない。
- 例){y^2∂[x]^2 - 4x^2 ∂[y]^2}u = 0~~y∂[x]ξ + 2x∂[y]ξ = 0~~y∂[x]η - 2x∂[y]η = 0と変換すると、~~∂[ξ]∂[η]u = (1/(2(ξ^2-η^2)))(η∂[ξ]-ξ∂[η])u
- 偏微分方程式の解法、
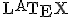 の練習
の練習
- 変数分離法
線形・同次な偏微分方程式で、境界条件も同次なときにはそのまま変数分離可能。
独立変数ごとの別々な関数の積の形で解を書いてから、境界条件を満たすような重みで重ね合わせる。
方程式や境界条件が同次でないときには、非同次の特解と同次の一般解を重ね合わせればいい。
- 有限長の一次元熱伝導
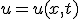
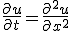
境界値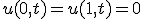
初期値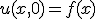
与えられた境界値条件(B.C.,Boundary Condition)と初期条件(I.C.,Initial Condition)のもとで
偏微分方程式の解を求める問題。初期値・境界値問題。
解の一意性は他で示すとして、発見的に解を見つける。
変数分離、 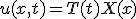 という形の解を仮定すると
という形の解を仮定すると
T,Xは、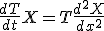 を満たす。
を満たす。
変形して、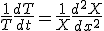
左辺は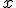 に依存せず、右辺は
に依存せず、右辺は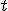 に依存しないので、両辺は定数でなければならない。
に依存しないので、両辺は定数でなければならない。
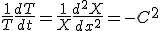
二つの別々な常微分方程式に帰着できた。
まず、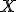 の方を解くと。
の方を解くと。
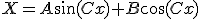
境界条件を課せば、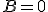 ~、
~、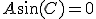
自明でない解は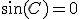 、
、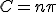 のときのみ存在し、
のときのみ存在し、
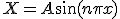
次に、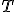 の方を解くと、
の方を解くと、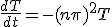
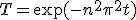
二つ合わせて、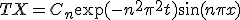
これは境界条件を満たす解の一系列になっている。
次に、元々の偏微分方程式が線形であることに注意して、初期条件を満たすために
得られた解の線形結合をとる。
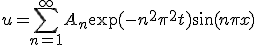
初期条件を満たすように係数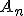 を決めれば最終的な解が求まる。
を決めれば最終的な解が求まる。
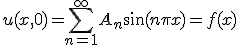

- 半無限長の一次元熱伝導
境界条件を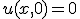 、
、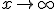 で
で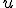 が有界、にする。
が有界、にする。
それ以外は同じ。
変数分離をして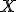 の方を解くと、
の方を解くと、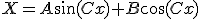
境界条件から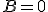 、
、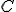 は任意の実数でよい。
は任意の実数でよい。
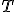 の方も解いてから重ね合わせると、
の方も解いてから重ね合わせると、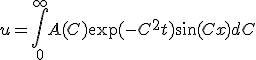
境界条件を満たすように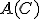 を決めると、
を決めると、
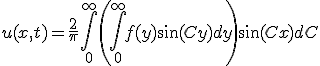
- 熱源のある有限長一次元熱伝導
熱源の無いときの偏微分方程式に項を追加して、
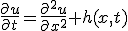 とする。他の条件は同じ。
とする。他の条件は同じ。
特解を見つけるために、定数変化法を使う。
同次方程式の解、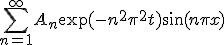 を少し一般化して、
を少し一般化して、
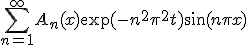 の形で探してみる。
の形で探してみる。
偏微分法定式に代入してみると。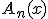 が満たすべき方程式は、
が満たすべき方程式は、
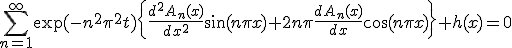
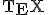 化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
非同次の一般解が得られる。
- フーリエ変換による解法
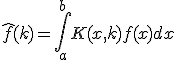 という形の関数から関数への線形変換を積分変換と呼ぶ。
という形の関数から関数への線形変換を積分変換と呼ぶ。
うまく変換すると方程式本体や境界条件を簡単にすることができる。
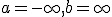
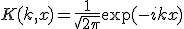 と選び、~
と選び、~
定義域を適当に設定したものをフーリエ変換と呼ぶ。
- 定義域が急減少超関数なら値域は緩増加関数。
定義域が緩増加超関数なら値域は急減少関数、などなど。少々うろ覚え。
- フーリエ変換
![\hat{f}(k) = F[f] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx](./cache/4e40dfd1bb5cd8af1bbbb6a71ef18e2a.mimetex.gif)
![f(x) = F^{-1}[\hat{f}] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{f}(k)e^{ikx}dk](./cache/2a1c4cc56c38d6c0b67b1e4653caa2af.mimetex.gif)
- 種々の公式
![F\left[\frac{d^n f}{dx^n}\right] = (ik)^{n}\hat{f}(k)](./cache/f2d727a7d520e28a127488e7945effa5.mimetex.gif)
![F[f*g] = \sqrt{2\pi}F[f]F[g]](./cache/7952637066706096cf7e8820336673fd.mimetex.gif)
![F[f\cdot g] = \frac{1}{\sqrt{2\pi}}F[f]*F[g]](./cache/cfde0161445b3d0d9bd6070d53e4f06d.mimetex.gif)
- 畳み込み
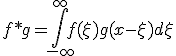
畳み込みは線形で可換、零関数以外との畳み込みは単射。
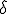 関数が単位元。
関数が単位元。
定数関数の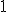 との畳み込みは全範囲での積分を表す。
との畳み込みは全範囲での積分を表す。
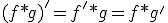
- 円形膜の振動。太鼓の中心を叩く。
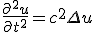
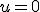 on
on 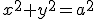
- 円筒座標系で波動方程式を解く。
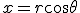
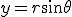
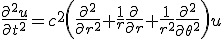
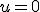 on
on 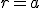
- 色々略。添付されているyambiさんのtexノート参照。
- 一般解は
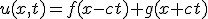
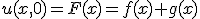
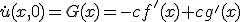
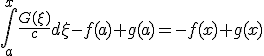
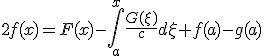
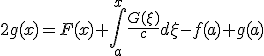
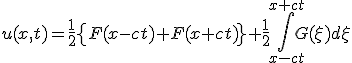
初期値が影響を与える領域は時間と共に広がってゆくが、有限の広さを持つ。
- 円板の平衡温度分布
- 半径
 の円板の円周上での温度分布がわかっているとき、
の円板の円周上での温度分布がわかっているとき、
平衡状態での内部の温度分布を求める。
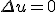
境界条件として、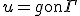
- 軸対称な問題なので、極座標で考える。極座標に移れば、
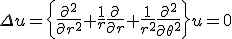
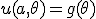
変数分離して、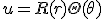
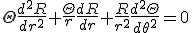
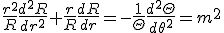
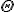 は周期性を持つ必要があるので、
は周期性を持つ必要があるので、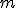 は非負整数。
は非負整数。
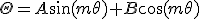
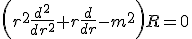
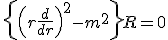
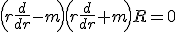
Rが原点で有界であることを課せば、
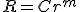
得られた解の群を重ね合わせて一般解を作れば、
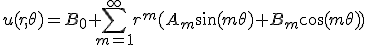
境界条件を満たすように係数を決めると、
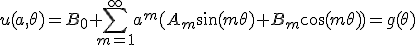
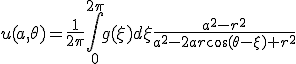
- ラプラス方程式
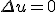 の解を、調和関数と呼ぶ。
の解を、調和関数と呼ぶ。
- 「調和関数の平均値の定理」が成り立つ。
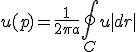 、
、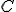 はpを中心とする半径aの円。
はpを中心とする半径aの円。
三次元では、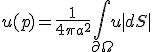 、
、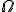 はpを中心とする半径aの球。
はpを中心とする半径aの球。
- 最大・最小の定理
定数でない調和関数は領域内部では極大・極小をとらない。
- ラプラス方程式、ディリクレ境界問題の解の一意性。境界での関数値を指定する。
2つの解の存在を仮定すると、その差もラプラス方程式を満たし、差は境界で0となる。
ラプラス方程式の解は境界でのみ最大値・最小値を取れるので、最大値も最小値も0。
よって2解の差は常に0となり、一致する。
- 1階常微分方程式の初期値問題の数値解法
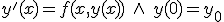
- オイラー法
非常に単純。精度はとても悪い。
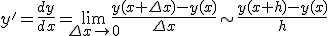
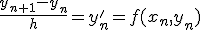
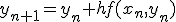
- 精度の向上
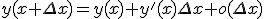
オイラー法では、解のテイラー展開のうち、
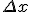 の一次までとって他を無視している。
の一次までとって他を無視している。
もっと高次の項までとれば解の精度がよくなる。
なるべく手間をかけずに高階微分の項を取り入れる方法を探す。
- 4次のRunge-Kutta法
xをずらした点の値を使って、高階微分の項を取り入れる。
- 数値積分の利用
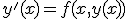 の両辺を
の両辺を![[x_n,x_{n+1}]](./cache/702b31de21f4beeac716f105712526ff.mimetex.gif) の区間で積分すると、
の区間で積分すると、
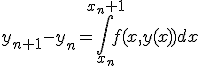
右辺には未知関数の積分が入っているのですぐには値を求められない。
右辺を長方形近似したものがオイラー法。
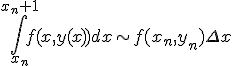
まずオイラー法で予測子として仮の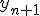 の値を求め、
の値を求め、
台形公式で近似するのがホイン法。
現在の値と1ステップ前の値から直線近似で次の値を求めるのがアダムス・バッシュフォース法
- 連立微分方程式と高階微分方程式の初期値問題
- 連立微分方程式
既知の初期値から始まり、微分が既知の関数として与えられている。
解法は1変数のときと同じ
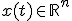
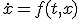
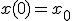
- オイラー法
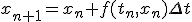
- ホイン法
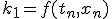
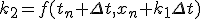
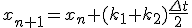
- 4次Runge-Kutta法
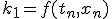
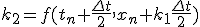
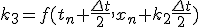
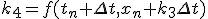
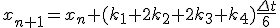
- 高階微分方程式
高階の微分方程式は変数を増やすことで連立微分方程式に帰着可能
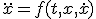 は
は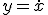 と置けば
と置けば
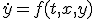
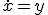
- 数値微分
離散的なサンプル値だけが既知の関数の微係数の近似値を計算する。
- 求めたい点の周りの関数値の線形結合で微係数を近似計算する。
周り3点を使うと、
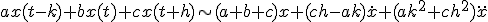
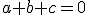
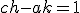 と選べば近似値が得られ、
と選べば近似値が得られ、
さらに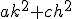 とすれば精度が上がる。
とすれば精度が上がる。
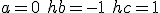 と選んだものを前進差分。
と選んだものを前進差分。
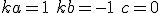 と選んだものを後退差分。
と選んだものを後退差分。
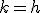 のときに
のときに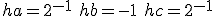 と選んだものを中心差分と呼ぶ。
と選んだものを中心差分と呼ぶ。
- 境界値問題
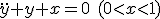
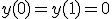 と、
と、
領域の境界での制約が与えられた問題を境界値問題と呼ぶ。
今回の微分方程式の一般解は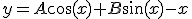
境界条件を課すと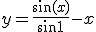
- 差分法による近似解法
空間を離散化し、格子点上での近似解を求める。
各格子点に番号を振り、微分を差分で置き換えて、
微分方程式を差分方程式に近似する。
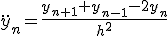
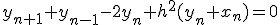
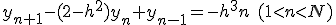
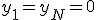
線形微分方程式を連立一次方程式に変換できた。
この方程式は対角要素とその上下一つだけが非ゼロの帯状行列。
対角より下の要素を消すように掃き出し、後退代入で下から値を定めていけば
 で解ける。
で解ける。
- 偏微分方程式の差分解法
- 1次元拡散方程式の陽解法
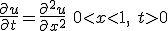
境界条件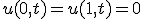 と
と
初期条件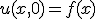 の
の
両方が与えられている問題は初期値境界値問題。
問題を解く領域を固定して、時間・空間を等間隔に離散化し、
偏微分を差分に置き換える。
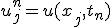
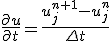
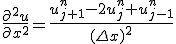
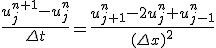
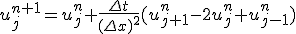
これはnについての漸化式。初期値と境界値が決まれば次々に決めて行くことができる。
差分近似で刻み幅を大きくとりすぎてしまうと解が振動してしまい、
誤差がどんどん大きくなってしまう。
この熱伝導方程式の場合、その境目は0.5。
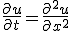 に
に
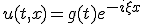 の形の解を仮定すると、
の形の解を仮定すると、
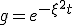 が得られる。
が得られる。
差分方程式の方にも特解として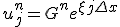 の形の解を仮定する。
の形の解を仮定する。
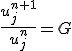 は増幅率と呼ばれる。
は増幅率と呼ばれる。
差分方程式が有界な解を持つためには、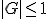 が必要。
が必要。
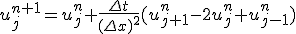
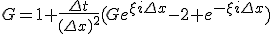
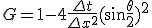
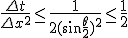 ならば解は収束する。
ならば解は収束する。
- 陰解法
時間微分を差分に直す際、前進差分ではなく後退差分を取ってみる。
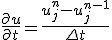
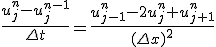
これは、漸化式型ではなく、連立一次方程式になっている。
陰解法では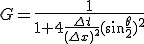 、刻み幅の取り方に依らずに安定。
、刻み幅の取り方に依らずに安定。
陰解法と陽解法を組み合わせて、
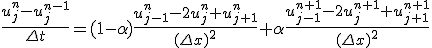
と取ると、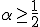 のとき
のとき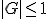 になる。
になる。
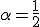 のとき時間精度が一つ向上する。
のとき時間精度が一つ向上する。
- ADI法(Alternating Direction Implicit Method)
二次元の熱伝導方程式の陰解法では、巨大な疎行列がかかった連立一次方程式が現れる。
計算時間を削減するために、特定の方向だけを陰的に、他の方向を陽的にし、
各ステップで陰的にする方向を交互に切り替えて計算すると
計算量を削減しつつ安定性を確保できる。
2次元ならうまくいくが、3次元ではこの方法では安定性は確保できない。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
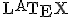 の練習
の練習
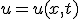
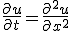
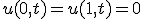
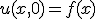
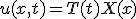 という形の解を仮定すると
という形の解を仮定すると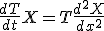 を満たす。
を満たす。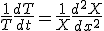
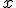 に依存せず、右辺は
に依存せず、右辺は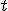 に依存しないので、両辺は定数でなければならない。
に依存しないので、両辺は定数でなければならない。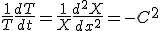
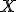 の方を解くと。
の方を解くと。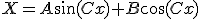
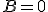 ~、
~、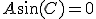
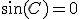 、
、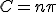 のときのみ存在し、
のときのみ存在し、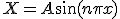
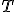 の方を解くと、
の方を解くと、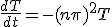
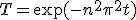
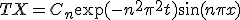
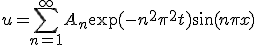
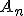 を決めれば最終的な解が求まる。
を決めれば最終的な解が求まる。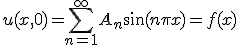

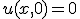 、
、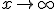 で
で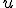 が有界、にする。
が有界、にする。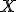 の方を解くと、
の方を解くと、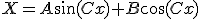
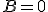 、
、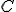 は任意の実数でよい。
は任意の実数でよい。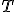 の方も解いてから重ね合わせると、
の方も解いてから重ね合わせると、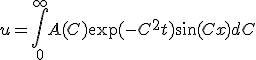
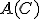 を決めると、
を決めると、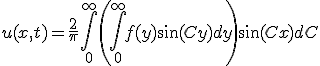
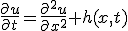 とする。他の条件は同じ。
とする。他の条件は同じ。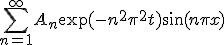 を少し一般化して、
を少し一般化して、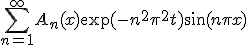 の形で探してみる。
の形で探してみる。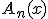 が満たすべき方程式は、
が満たすべき方程式は、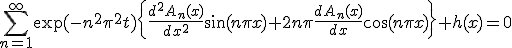
 化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば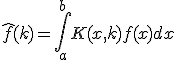 という形の関数から関数への線形変換を積分変換と呼ぶ。
という形の関数から関数への線形変換を積分変換と呼ぶ。
 と選び、~
と選び、~![\hat{f}(k) = F[f] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx](./cache/4e40dfd1bb5cd8af1bbbb6a71ef18e2a.mimetex.gif)
![f(x) = F^{-1}[\hat{f}] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{f}(k)e^{ikx}dk](./cache/2a1c4cc56c38d6c0b67b1e4653caa2af.mimetex.gif)
![F\left[\frac{d^n f}{dx^n}\right] = (ik)^{n}\hat{f}(k)](./cache/f2d727a7d520e28a127488e7945effa5.mimetex.gif)
![F[f*g] = \sqrt{2\pi}F[f]F[g]](./cache/7952637066706096cf7e8820336673fd.mimetex.gif)
![F[f\cdot g] = \frac{1}{\sqrt{2\pi}}F[f]*F[g]](./cache/cfde0161445b3d0d9bd6070d53e4f06d.mimetex.gif)
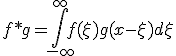
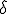 関数が単位元。
関数が単位元。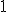 との畳み込みは全範囲での積分を表す。
との畳み込みは全範囲での積分を表す。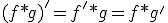
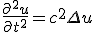
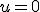 on
on 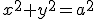
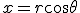
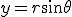
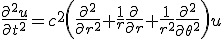
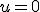 on
on 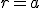
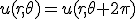
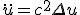
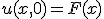
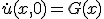
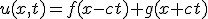
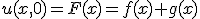
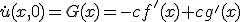
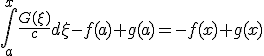
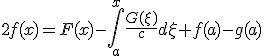
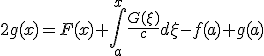
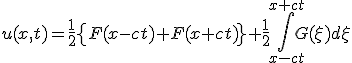
 の円板の円周上での温度分布がわかっているとき、
の円板の円周上での温度分布がわかっているとき、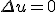
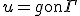
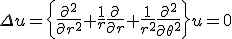
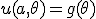
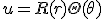
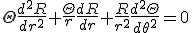
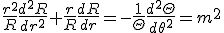
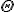 は周期性を持つ必要があるので、
は周期性を持つ必要があるので、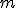 は非負整数。
は非負整数。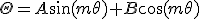
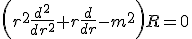
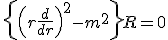
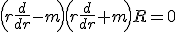
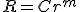
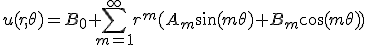
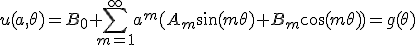
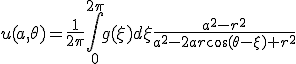
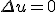 の解を、調和関数と呼ぶ。
の解を、調和関数と呼ぶ。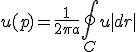 、
、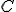 はpを中心とする半径aの円。
はpを中心とする半径aの円。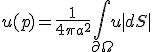 、
、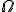 はpを中心とする半径aの球。
はpを中心とする半径aの球。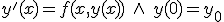
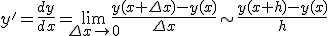
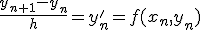
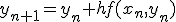
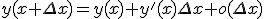
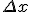 の一次までとって他を無視している。
の一次までとって他を無視している。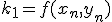
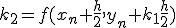
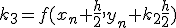
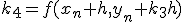
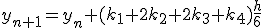
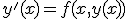 の両辺を
の両辺を![[x_n,x_{n+1}]](./cache/702b31de21f4beeac716f105712526ff.mimetex.gif) の区間で積分すると、
の区間で積分すると、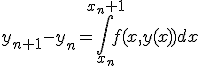
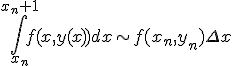
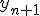 の値を求め、
の値を求め、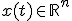
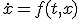
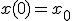
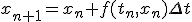
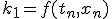
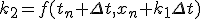
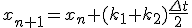
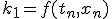
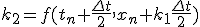
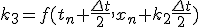
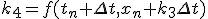
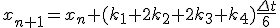
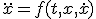 は
は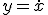 と置けば
と置けば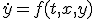
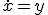
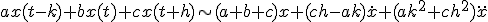
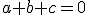
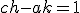 と選べば近似値が得られ、
と選べば近似値が得られ、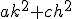 とすれば精度が上がる。
とすれば精度が上がる。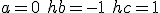 と選んだものを前進差分。
と選んだものを前進差分。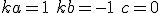 と選んだものを後退差分。
と選んだものを後退差分。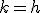 のときに
のときに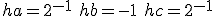 と選んだものを中心差分と呼ぶ。
と選んだものを中心差分と呼ぶ。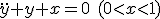
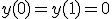 と、
と、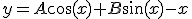
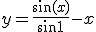
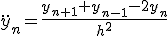
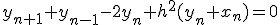
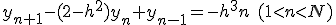
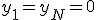
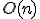 で解ける。
で解ける。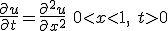
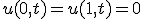 と
と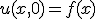 の
の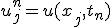
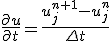
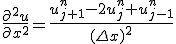
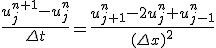
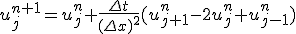
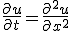 に
に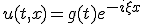 の形の解を仮定すると、
の形の解を仮定すると、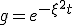 が得られる。
が得られる。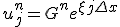 の形の解を仮定する。
の形の解を仮定する。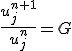 は増幅率と呼ばれる。
は増幅率と呼ばれる。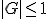 が必要。
が必要。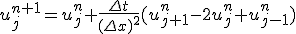
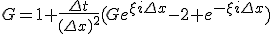
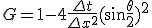
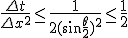 ならば解は収束する。
ならば解は収束する。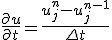
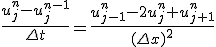
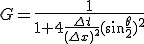 、刻み幅の取り方に依らずに安定。
、刻み幅の取り方に依らずに安定。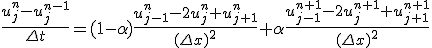
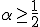 のとき
のとき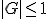 になる。
になる。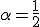 のとき時間精度が一つ向上する。
のとき時間精度が一つ向上する。