![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
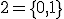
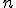 変数論理関数、
変数論理関数、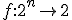 ブール関数・スイッチング関数とも呼ばれる。
ブール関数・スイッチング関数とも呼ばれる。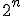 全てについて値が定義されているものを、完全定義関数。
全てについて値が定義されているものを、完全定義関数。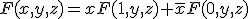 と展開すれば、2変数論理関数2つに分解できる。
と展開すれば、2変数論理関数2つに分解できる。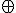 (XOR,exclusive or,対称差)を
(XOR,exclusive or,対称差)を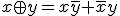 で定義する。
で定義する。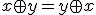
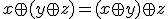 ~
~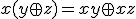
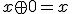
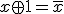
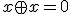
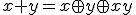 が成立。
が成立。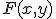 について、
について、と展開できる。繰り返して展開すると、論理変数からいくつか取り出して
積を作った2^n個の項の排他的論理和として表現できる。
この展開をリード・マラー展開やガロア標準形と呼ぶ。
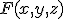 の否定は、
の否定は、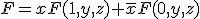
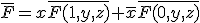
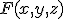 が
が について正であるとは、
について正であるとは、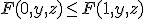 、「左辺が真で右辺が偽」とはならない論理関数。
、「左辺が真で右辺が偽」とはならない論理関数。 に関して正な関数については、
に関して正な関数については、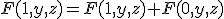 が成立。
が成立。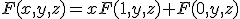 と分解できる。
と分解できる。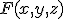 について、
について、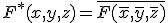 を
を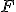 の双対関数と呼ぶ。
の双対関数と呼ぶ。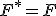 となる関数は自己双対関数。
となる関数は自己双対関数。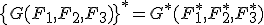
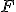 について、変数
について、変数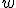 を一つ追加した
を一つ追加した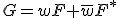 は自己双対。
は自己双対。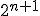 種類、
種類、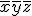
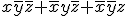
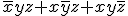
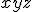
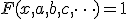 の解
の解 は?
は?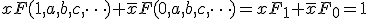
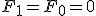 のとき、解なし。
のとき、解なし。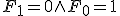 のとき、
のとき、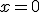
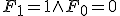 のとき、
のとき、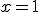
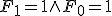 のとき、
のとき、 は任意。
は任意。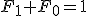 と書ける。
と書ける。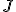 で表すと、解
で表すと、解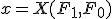 は、
は、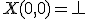
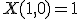
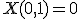
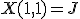
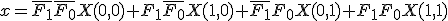
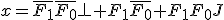 であり、
であり、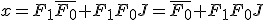 と書ける。
と書ける。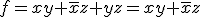
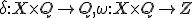
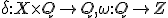 出力が状態のみに依存。出力は遷移後。
出力が状態のみに依存。出力は遷移後。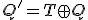
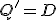
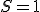 なら
なら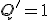 に、
に、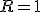 なら
なら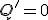 にする。
にする。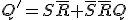
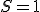 かつ
かつ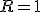 は禁止入力。
は禁止入力。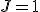 なら
なら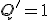 に、
に、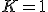 なら
なら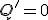 にする。
にする。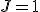 かつ
かつ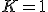 ならばトグル。
ならばトグル。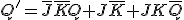
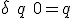
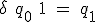
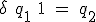
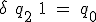
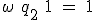
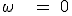
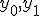 、状態割り当ては、
、状態割り当ては、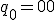
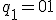
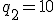 とすると、
とすると、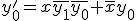
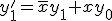
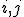 にもう一つ入力を与えてやったときに
にもう一つ入力を与えてやったときに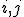 はs+1次等価。
はs+1次等価。