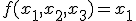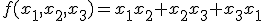講義日程-2007年度冬学期
計算システム論第一 †
- 担当:南谷 崇 教授
- 1.5単位
- 14:45-16:15 工学部六号館 62講義室
- 出席あり(救済措置的)
- 参考書
内容 †
- VLSI計算システム概論
- ハードウェアの経年劣化と同様に、ソフトウェアも経年劣化する。~~信頼性を保つためには常にメンテナンスが必要。~~これを怠るとインターフェイスに齟齬が生じ、あちこちに不具合が現れる。
- 以下、いろいろ要約すると「電力消費・情報転送量多すぎ。無駄な情報流さず、もっと節約せい。」
- 論理回路
- 計算機の素子は基本的にはAND,OR,NOTでできている。(実際にはNANDだけで他を構成している)
- ブール代数と論理回路
- 順序集合~~反射律、対称律、推移律を満たす二項関係を伴う集合。~~最大元があればそれを1、最小元があればそれを0とする。その集合を
- 束の公理~~冪等で可換、結合的な二項演算で、吸収律を満たすものを伴う集合。~~さらに分配律を満たす束を分配束と呼ぶ。
- ブール代数の公理~~最大元と最小元を持った分配束に、二十否定除去、相補性とドモルガン律を満たす単項演算を入れたもの。
- 双対性原理~~ブール代数の式について、項を全て否定し、+を・に、・を+に置き換えた式を双対な論理式と呼ぶ。~~ブール代数では、任意の等式とその双対等式について、片方が成り立てばもう片方も成り立つ。
- 論理関数
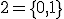
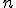 変数論理関数、
変数論理関数、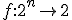 ブール関数・スイッチング関数とも呼ばれる。
ブール関数・スイッチング関数とも呼ばれる。
表現形式としては、論理式・真理値表・キューブ表現・BDDがある。
定義域の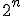 全てについて値が定義されているものを、完全定義関数。
全てについて値が定義されているものを、完全定義関数。
値が未定義の組み合わせがあり、「渡してはいけない値」があるものを、不完全定義関数と呼ぶ。
- 論理式の表現には真理値表が最も簡単。
ROMの入力値に対応する論理値を書き込んで
真理値表を作れば、簡単に論理回路を作れる。
ただし、入力変数が増えると表の行数が急激に増える。
- 論理式による表現。
論理関数は必ず論理式で書けるか?Yes.
- ブール展開
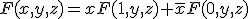 と展開すれば、2変数論理関数2つに分解できる。
と展開すれば、2変数論理関数2つに分解できる。
同様に展開を進めると、引数の積と否定からなる項の和からなる形の論理式として、この論理関数を表現できる。
ある項を真にする論理変数の組み合わせが唯一であるとき、その項は極小項と呼ばれる。
全ての論理変数の積を取ったものと、そのうちいくつかの論理変数を否定したものが極小項。
極小項の和で書かれた論理式は、真理値表と一対一対応。積和表現。
積和表現の双対として、極小項の双対である極大項の積で表現した和積表現も真理値表と一対一。
積和表現は、もとの論理関数を否定したものを積和表現で表して、ド・モルガン則で元に戻せば得られる。
- リード・マラー展開
排他的論理和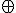 (XOR,exclusive or,対称差)を
(XOR,exclusive or,対称差)を
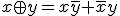 で定義する。
で定義する。
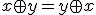
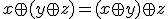 ~
~
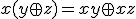
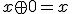
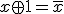
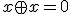
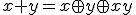 が成立。
が成立。
2変数論理関数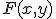 について、
について、
と展開できる。繰り返して展開すると、論理変数からいくつか取り出して
積を作った2^n個の項の排他的論理和として表現できる。
この展開をリード・マラー展開やガロア標準形と呼ぶ。
- キューブ表現
トランジスタの配置パターンそのままで表現。
各項に論理変数とその否定に対応するビットを用意して、
項にその変数が現れるならビットを立てる。
- BDD(Binary Decision Diagram)
- 論理式の真偽値表をツリー表現。標準化して冗長性を除く。
標準化されたグラフは、評価する順番を固定すると一意に定まる。
ほとんどの論理式はグラフ表現にして簡約すれば簡単な形になる。
- 論理関数の否定
- 多くの論理変数を含む論理式をドモルガン律を使って否定しようとすると、項数がとても多くなる。
- 論理関数
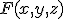 の否定は、
の否定は、
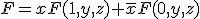
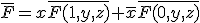
- ユネイト関数
各変数が、肯定形か否定形かのどちらかしか現れない積和形式で表される論理関数。
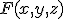 が
が について正であるとは、
について正であるとは、
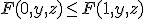 、「左辺が真で右辺が偽」とはならない論理関数。
、「左辺が真で右辺が偽」とはならない論理関数。
 に関して正な関数については、
に関して正な関数については、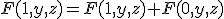 が成立。
が成立。
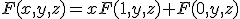 と分解できる。
と分解できる。- xについて負な関数についても同様。
- すべての変数に関して(正/負)な関数は単調(増大/減少)関数。エラー検出について有用。
- 自己双対関数
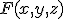 について、
について、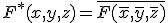 を
を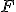 の双対関数と呼ぶ。
の双対関数と呼ぶ。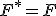 となる関数は自己双対関数。
となる関数は自己双対関数。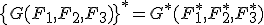
- 任意の関数
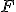 について、変数
について、変数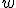 を一つ追加した
を一つ追加した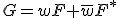 は自己双対。
は自己双対。
- 対称関数
任意の変数同士を置換しても変化しない関数。
- 任意の対称関数は基本対称関数の線形結合で表される。
n変数での対称関数は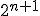 種類、
種類、
3変数では
- ブール代数方程式
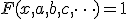 の解
の解 は?
は?
ブール展開して、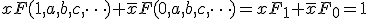
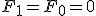 のとき、解なし。
のとき、解なし。
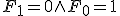 のとき、
のとき、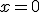
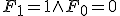 のとき、
のとき、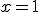
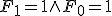 のとき、
のとき、 は任意。
は任意。
解の存在条件は、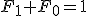 と書ける。
と書ける。- 『任意』を
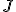 で表すと、解
で表すと、解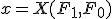 は、
は、
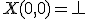
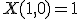
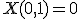
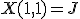
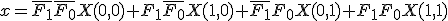
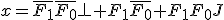 であり、
であり、
解が存在するなら、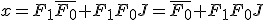 と書ける。
と書ける。
- 論理合成
- 真理値表がベース。まず標準形で書いてから最適化する。
- Karnaugh図を用いる。
真理値表を並び替え、Hamming距離が1になる値が隣り合うようにすると、
積和標準形での各項が図の上で近くに固まり、項を視覚的に表現できる。
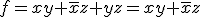
- Hamming距離:異なるビットの数を距離と見たもの。
- Quine-Mcluskeyの方法
- 積和形論理式の主項を生成する。
主項とは、項に積として含まれる部分のうち、
どれを落としても全体の論理式を満たせないもの。
カルノー図上では、それ以上広げられない塊。
最も単純な表現の論理式は、主項だけからなる。
最も大きな主項が含まれるとは限らない。
- 最小項を全て列挙し、各ハミング距離1の組について、
その項がまとめられるかどうかをチェックし、まとめられる組は全て生成する。
まとめることができた項を除き、再び各ハミング距離1の組について同じようにまとめる。
これをまとめるべき項がなくなるまで繰り返せば、主項を全て得られる。
- 主項からいくつかを選んで、最小項全てを覆うようにすれば、
それが最も項の少ない積和形論理式の表現になっている。
- 3段NAND形式
- 否定の入った積和形式はNAND素子三段で実装できる。
否定回路には、本来2入力のNAND素子に定入力を与えてしまっている。
最初からNANDのみを使って回路を作れば、段数を稼ぐことができる。
- 2線論理
- 1線式の通常の論理回路では、論理変化を追うことはできない。
出力が計算結果なのか遅延の影響なのかがわからない。
値とその否定をペアにして、2線を同時に扱うと、
クロックを使わずに回路をつくれ、回路は単調増加回路になる。
配線の量は倍になるが、否定は線の入れ替えだけで作れるので、
素子の数は倍にはならない。
- 順序回路
内部状態を持った回路。順序回路。有限状態機会。
入力X,出力Zの他に内部状態Qをもっていて、遷移関数で特徴づけられる。
Mealyモデル: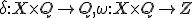
Mooreモデル: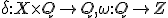 出力が状態のみに依存。出力は遷移後。
出力が状態のみに依存。出力は遷移後。
二つの状態が、任意の入力に対して同じ出力を返し同じ状態に移動するなら、同じ状態。
- 順序回路は状態遷移図・状態遷移表で表現される。
- 順序回路の実装には、出力用の組み合わせ回路,状態遷移用の組み合わせ回路,記憶素子を使う。
- 記憶素子
- 記憶素子はフリップフロップの構造を持つ回路の集まり。
内部状態を持つ回路には初期化の機能が必須。
- T型フリップフロップ
JKフリップフロップのJとKをつないで同じ値にしたものと等価。
入力の立ち上がりと立ち下がりを検出し、立ち下がりの時に出力を反転させる。
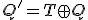
- D型フリップフロップ
入力を1クロック文遅延させて出力する。
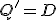
- SR型
S(Set)とR(Reset)の2入力フリップフロップ。
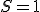 なら
なら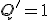 に、
に、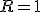 なら
なら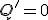 にする。
にする。
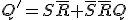
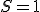 かつ
かつ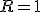 は禁止入力。
は禁止入力。
- JKFF
最も多用される順序回路。
JとKの2入力フリップフロップ。SR型とT型を合わせた特性。
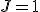 なら
なら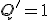 に、
に、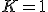 なら
なら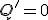 にする。
にする。
ただし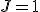 かつ
かつ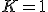 ならばトグル。
ならばトグル。
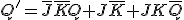
- マスタ・スレーブ型ラッチ
クロックの変化を待たずに出力が入力に戻ってしまうのを防ぐために、記憶素子を2重にする。
- 順序回路の難しさ。
ゲート遅延や配線遅延のため、過渡的に内部状態が乱れ、
それを記憶素子が記憶してしまい、回路が誤動作を起こすことがある。
信号の遅延には素子の配置や配線が影響してくるので回路図だけからは予測が難しい。
- 3進カウンタ
累積で3回1が入力されたら1回だけ1を出力して初期状態にもどる回路。
- 状態遷移
状態は3種類。
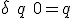
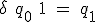
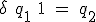
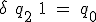
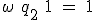
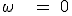
内部状態は2bit変数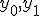 、状態割り当ては、
、状態割り当ては、
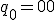
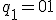
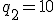 とすると、
とすると、
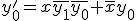
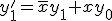
- 順序回路の等価性
完全定義な順序回路について、
長さsの入力で区別できない二つの状態はs次等価であるという。
任意の長さの入力で区別できない二つの状態は等価であるという。
s次等価な状態で、全状態を分割したときに、
同じ分割に属する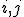 にもう一つ入力を与えてやったときに
にもう一つ入力を与えてやったときに
別々な分割に遷移しないなら、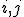 はs+1次等価。
はs+1次等価。
- Boothの乗算アルゴリズム
- 乗数中に1が続くときに、引き算を使って1の数を減らし、
乗算時に使う加算の回数を減らす。
- 乗数を下位ビットから順に見て行き、現在見ているビットが
一つ前のビットと同じならば何もしない。
1になったら結果から被乗数を引く、0になったら結果に被乗数を足す。
結果を1ビット左にシフト。
multiply(A,B){
P = 0;
b = 0;
repeat(N){
case(A[0],b){
(01)-> P += B;
(10)-> P -= B;
}
(P,A,b) >>= 1;
}
return (P,A);
}
Presented by yambi. tzik all blame reserved.
誤植は見つけた人が直してね
- 1 任意の
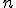 変数論理関数
変数論理関数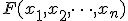 とその双対関数
とその双対関数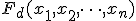 を用いて得られる
を用いて得られる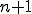 変数論理回路
は自己双対であることを証明せよ.
変数論理回路
は自己双対であることを証明せよ.
- 解
なので明らかに自明であることは明白より明らか.
- 2 次のように定義される関数
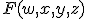 のもっとも簡単な積和論理式を全て示せ.
のもっとも簡単な積和論理式を全て示せ.
yz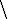 wx wx | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 0 | 0 |
| 01 | 1 | 1 | 0 | 1 |
| 11 | 1 | 1 | 1 | 1 |
| 10 | 0 | 0 | 1 | 1 |
- 解
カルノー図を眺め,感より
の2つだろうと思いたい.
- 3 1を3回続けて入力したときのみ1を出力する1入力1出力同期式順回路をDFFを用いて設計する過程を示せ.
その結果をAND, OR, NOT及びDFFを基本素子とする最も簡単な論理回路図で示せ.
ただし,入力信号を
 ,出力信号を
,出力信号を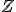 とする.
とする.
- 解
3回続けて入力したかどうかを判定することは2つの状態ではできないことは明らか.
状態遷移表はstateを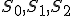 とし隣接行列で書くと(動作/イベント)
とし隣接行列で書くと(動作/イベント)
現段階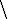 次段階 次段階 | 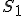 | 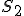 | 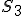 |
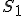 | 0/0 | 0/1 | - |
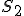 | 0/0 | - | 0/1 |
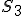 | 0/0 | - | 1/1 |
と書ける.
状態数が2ビットで表現できることより,DFFを2つ(A,Bとする)用いて表現できる.
よって,内部状態を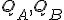 とし,
状態
とし,
状態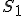 を
を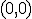
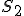 を
を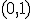
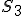 を
を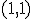 とし,状態遷移表を書き直すと(イベント/次の状態)
とし,状態遷移表を書き直すと(イベント/次の状態)
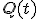 | 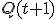 |
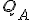 | 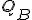 | X=0 | X=1 |
| 0 | 0 | 0/00 | 0/01 |
| 0 | 1 | 0/00 | 0/11 |
| 1 | 1 | 0/00 | 1/11 |
| 1 | 0 | - | - |
以上より同期式順序回路は
DFF Aの入力を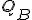 ,
DFF Bの入力を
,
DFF Bの入力を ,
出力
,
出力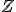 を
を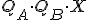 としたものである.
としたものである.
- 4 8ビットレジスタを用いた符合付き「2の補数」表示の2進加算に関して以下の問いに答えよ.
- (1) 一つのレジスタに収容できる整数の範囲を10進数で示せ.
- 解
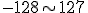 .
.
一般に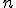 ビットレジスタを用いれば
ビットレジスタを用いれば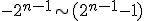 までの整数を収容できる.
までの整数を収容できる.
- (2) 演算「89-76」はどのように実行されるかを説明せよ.
- 解
89は2進数表示で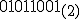 ,
76は2進数表示で
,
76は2進数表示で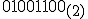 なので,
なので,
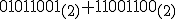 を計算すれば良い.
オーバーフローは無視をする.
を計算すれば良い.
オーバーフローは無視をする.
- (3) 一般に,結果にオーバーフローが生じるのはどのような場合かを符号ビットへのキャリー(C7)と符号ビットからのキャリー(C8)に関連して説明せよ.
- 解
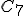 | 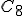 | 状況 |
| 0 | 0 | 正と正または正と負(または負と正)の足し算でオーバーフローが生じないとき. |
| 0 | 1 | 正と正の足し算でオーバーフローが生じたとき. |
| 1 | 0 | 負と負の足し算でオーバーフローが生じたとき. |
| 1 | 1 | 負と負または正と負の足し算でオーバーフローが生じないとき |
- 5 以下の各演算について,その方法と特徴を簡潔に説明せよ.
- (1) キャリールックアヘッド加算
- 解
通常の加算器(リップルアダー)では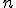 ビットの足し算を行うために
ビットの足し算を行うために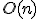 段の計算が必要であるが,キャリーを先読みするようにすれば段数を減らすことができる.
段の計算が必要であるが,キャリーを先読みするようにすれば段数を減らすことができる.
段数は定数オーダまで減らすことができるが必要な素子数が指数的に増えてしまう.
として,
とすれば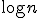 ,素子数は
,素子数は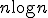 で構成できバランスが良い.
で構成できバランスが良い.
- (3) Boothの乗算アルゴリズム
- 解
2の補数表現の符号付整数乗算の手法の一つ.
連続する2ビットに着目しその4通りのパターンに従って操作を行うもの.
これを拡張し,同時に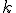 ビットを同時にみることにすれば
ビットを同時にみることにすれば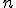 ビットの掛け算に
ビットの掛け算に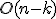 の計算しか必要なくなると思うが,この文章は疑わしい.
の計算しか必要なくなると思うが,この文章は疑わしい.
- 自己双対論理関数の定義
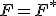 となるような関数.すなわち(0と1),(
となるような関数.すなわち(0と1),( と
と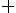 )を取り替えても変わらないような関数.
)を取り替えても変わらないような関数.
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
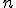 変数論理関数、
変数論理関数、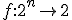 ブール関数・スイッチング関数とも呼ばれる。
ブール関数・スイッチング関数とも呼ばれる。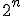 全てについて値が定義されているものを、完全定義関数。
全てについて値が定義されているものを、完全定義関数。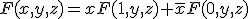 と展開すれば、2変数論理関数2つに分解できる。
と展開すれば、2変数論理関数2つに分解できる。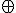 (XOR,exclusive or,対称差)を
(XOR,exclusive or,対称差)を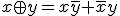 で定義する。
で定義する。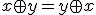
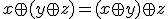 ~
~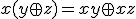
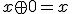
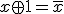
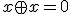
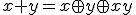 が成立。
が成立。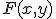 について、
について、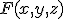 の否定は、
の否定は、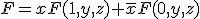
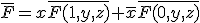
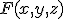 が
が について正であるとは、
について正であるとは、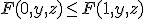 、「左辺が真で右辺が偽」とはならない論理関数。
、「左辺が真で右辺が偽」とはならない論理関数。 に関して正な関数については、
に関して正な関数については、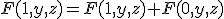 が成立。
が成立。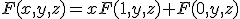 と分解できる。
と分解できる。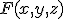 について、
について、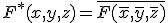 を
を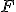 の双対関数と呼ぶ。
の双対関数と呼ぶ。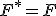 となる関数は自己双対関数。
となる関数は自己双対関数。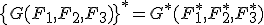
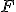 について、変数
について、変数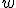 を一つ追加した
を一つ追加した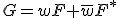 は自己双対。
は自己双対。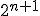 種類、
種類、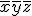
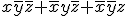
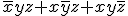
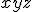
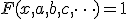 の解
の解 は?
は?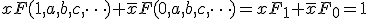
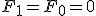 のとき、解なし。
のとき、解なし。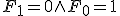 のとき、
のとき、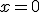
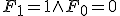 のとき、
のとき、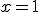
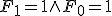 のとき、
のとき、 は任意。
は任意。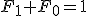 と書ける。
と書ける。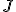 で表すと、解
で表すと、解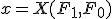 は、
は、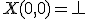
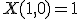
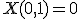
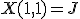
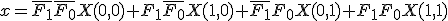
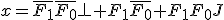 であり、
であり、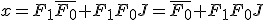 と書ける。
と書ける。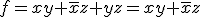
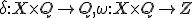
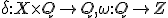 出力が状態のみに依存。出力は遷移後。
出力が状態のみに依存。出力は遷移後。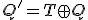
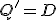
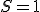 なら
なら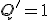 に、
に、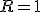 なら
なら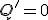 にする。
にする。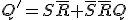
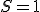 かつ
かつ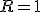 は禁止入力。
は禁止入力。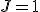 なら
なら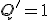 に、
に、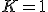 なら
なら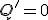 にする。
にする。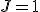 かつ
かつ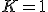 ならばトグル。
ならばトグル。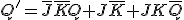
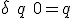
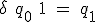
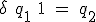
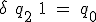
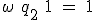
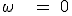
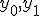 、状態割り当ては、
、状態割り当ては、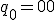
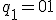
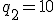 とすると、
とすると、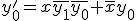
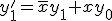
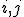 にもう一つ入力を与えてやったときに
にもう一つ入力を与えてやったときに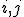 はs+1次等価。
はs+1次等価。
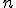 変数論理関数
変数論理関数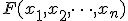 とその双対関数
とその双対関数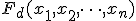 を用いて得られる
を用いて得られる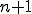 変数論理回路
変数論理回路
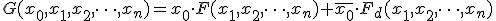
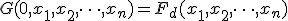
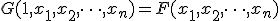
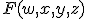 のもっとも簡単な積和論理式を全て示せ.
のもっとも簡単な積和論理式を全て示せ.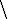 wx
wx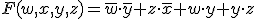
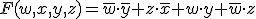
 ,出力信号を
,出力信号を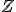 とする.
とする.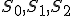 とし隣接行列で書くと(動作/イベント)
とし隣接行列で書くと(動作/イベント)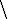 次段階
次段階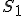
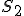
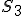
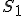
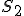
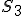
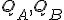 とし,
状態
とし,
状態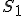 を
を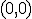
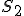 を
を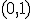
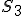 を
を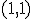 とし,状態遷移表を書き直すと(イベント/次の状態)
とし,状態遷移表を書き直すと(イベント/次の状態)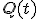
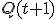
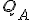
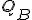
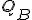 ,
DFF Bの入力を
,
DFF Bの入力を ,
出力
,
出力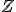 を
を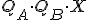 としたものである.
としたものである.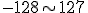 .
.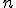 ビットレジスタを用いれば
ビットレジスタを用いれば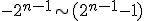 までの整数を収容できる.
までの整数を収容できる.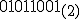 ,
76は2進数表示で
,
76は2進数表示で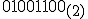 なので,
なので,
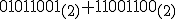 を計算すれば良い.
オーバーフローは無視をする.
を計算すれば良い.
オーバーフローは無視をする.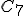
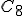
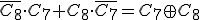
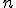 ビットの足し算を行うために
ビットの足し算を行うために 段の計算が必要であるが,キャリーを先読みするようにすれば段数を減らすことができる.
段の計算が必要であるが,キャリーを先読みするようにすれば段数を減らすことができる.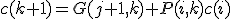
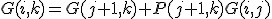
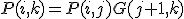
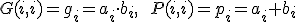
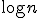 ,素子数は
,素子数は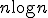 で構成できバランスが良い.
で構成できバランスが良い.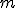 ),指数部(
),指数部( )を用いて表現して演算を行う.
この小数は
)を用いて表現して演算を行う.
この小数は を基数とし
を基数とし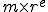 を表す.
を表す.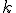 ビットを同時にみることにすれば
ビットを同時にみることにすれば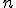 ビットの掛け算に
ビットの掛け算に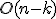 の計算しか必要なくなると思うが,この文章は疑わしい.
の計算しか必要なくなると思うが,この文章は疑わしい.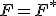 となるような関数.すなわち(0と1),(
となるような関数.すなわち(0と1),( と
と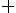 )を取り替えても変わらないような関数.
)を取り替えても変わらないような関数.