講義日程-2007年度冬学期
計算量理論(Computational Complexity) †
- 担当:今井 浩 教授
- 1.5単位
- 10:15~11:45 理学部7号館(化学教育東館)236号室
- 参考書
- Michael R. Garey and David S. Johnson
Computers and Intractability
A Guide to the Theory of NP-Completeness
W.H.Freeman and Co. NY. 1979
過去問 †
とかないのかなぁ…isのwikiがみつからない。ないのかなぁ
今井桂子さんは奥さんですか?
ここにあります.
予想問題 †
Presented by yambi. tzik all blame reserved.
(誰か何が出ると言っていたか知っている人は教えてください.yambiは授業に出てません.)
誤植は見つけた人が直してね
- 0-1ナップザック問題とは
- Instance 非負整数
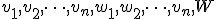
- Task
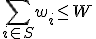 を満たし
を満たし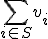 を最大化するような
を最大化するような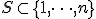 を求める.
を求める.
- PARTITION問題とは
- 0-1Knapsack問題のNP-hard性.
- PARTITION問題から多項式帰着する.
- PARTITION問題のInstance
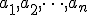 が与えられたとき,
が与えられたとき,
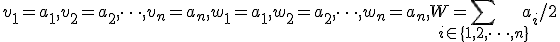 とする.
とする.
- このとき
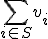 の最大値が
の最大値が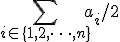 であるかどうかが分かればPARTITION問題が解ける.
であるかどうかが分かればPARTITION問題が解ける.
- この変換が多項式帰着であることは明らかなので0-1Knapsack問題はNP-hard
- 擬多項式時間アルゴリズム
- 動的計画法を用いる.
ただし,表の範囲外を参照されたら0を返すことにする.
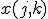 を
を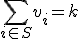 となるものの中での
となるものの中での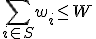 の最小値とする.ただし
の最小値とする.ただし とする.
とする.- このとき,表の埋め方は
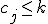 かつ
かつ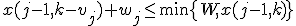 のときは
のときは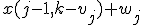 ,
それ以外のときは
,
それ以外のときは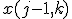 を埋めていく.
を埋めていく.
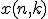 を走査すれば,何が選ばれたのかが分かる.
を走査すれば,何が選ばれたのかが分かる.- 計算時間は
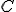 を最適解の値の上界として
を最適解の値の上界として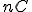 .
例えば
.
例えば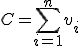 とできるが,これは擬多項式時間アルゴリズムである.
とできるが,これは擬多項式時間アルゴリズムである.
- KNAPSACK問題の
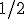 近似アルゴリズム.
近似アルゴリズム.
- アルゴリズム
を降順にソートし大きいものから順に
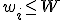 を満たすものを取り出し,
とする.ここで,整数
を満たすものを取り出し,
とする.ここで,整数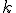 を
と定義する.このとき,
を
と定義する.このとき,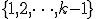 と
と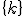 のうち
より良い方の解を選ぶ.(どちらも実行可能解であることに注意.)
のうち
より良い方の解を選ぶ.(どちらも実行可能解であることに注意.)
- 計算時間
ソートにかかる時間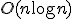 ,条件を満たす
,条件を満たす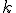 を求めるために
を求めるために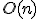 かかるので,合わせて
かかるので,合わせて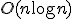 である.
多項式時間.
である.
多項式時間.
- 近似値比
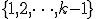 と
と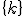 の二つの解の和は明らかに最適解以上のものとなっているので,近似値比は
の二つの解の和は明らかに最適解以上のものとなっているので,近似値比は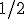 である.
である.
- KNAPSACK問題はFPTASである.
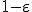 近似値比アルゴリズムが存在することを示せばよい.
近似値比アルゴリズムが存在することを示せばよい.- 具体的なアルゴリズム
- 2近似値比アルゴリズムによる解を
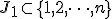 とする.
とする.
- 与えられた
 に対して,
に対して,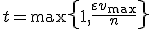 と置く.
と置く.
- 各要素について
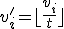 と修正したinstanceについて
と修正したinstanceについて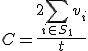 動的計画法を用いて得られる解を
動的計画法を用いて得られる解を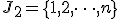 とする.
とする.
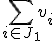 と
と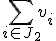 を比べ,大きいほうを出力する.また,その解を
を比べ,大きいほうを出力する.また,その解を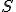 とする.
とする.
- 実行時間
動的計画法による計算時間が支配的.
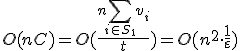 .
.
- 近似値比
最適解を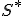 と書くことにすると,
と書くことにすると,
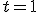 のときは,
のときは,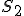 は最適解であり,そうでないときは上の不等式より
すなわち,
は最適解であり,そうでないときは上の不等式より
すなわち,
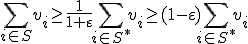 となるので
となるので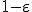 近似値比である.
近似値比である.
- 以上よりKNAPSACK問題はFPTAS
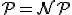 でない限り,KNAPSACK問題には,最適解と高々定数差しかない近似解を求める多項式時間アルゴリズムが存在しない.
でない限り,KNAPSACK問題には,最適解と高々定数差しかない近似解を求める多項式時間アルゴリズムが存在しない.
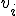 すべてに,十分大きい定数を掛けると近似解が最適解となるので
すべてに,十分大きい定数を掛けると近似解が最適解となるので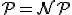 となる.
となる.
内容 †
- 計算量理論とは、計算の難しさの学問。
- 例)n都市TSP
n頂点の重み付き単純グラフ上の閉路で、各頂点をちょうど一度ずつ訪れる。
辺の重みの和を最小にする閉路を求める問題。
有限・離散なので解は有限時間内に計算可能。
しかしそのために必要な計算量は指数オーダー。
nが大きくなると実用時間内では実行不可能。
- 素朴な解法
(n-1)!通りの巡り方での距離を全て計算・比較。
路一つあたりの計算量が10^(-6)sでも、n=50くらいで計算量は10^50年。
- cf)ある頂点から他の全ての頂点への最短路を求める問題はO(|V|^2+|E|) Dijkstra's Algorithm
- TSPはどんなアルゴリズムでも、(最悪の場合)O(n^c)で解くことはできなさそう。NP問題
ミレニアム懸賞問題,P≠NP問題
- NP完全性の理論
- NP:Nondeterministic Polynomial,非決定性多項式時間
- n要素全順序集合のソーティング
- Insert Sort O(n^2)
- n個の整列されたリストにn+1個目の要素を適切な場所に挿入する。
- Bubble Sort O(n^2)
- Heap Sort O(n log n)
- Quick Sort 平均的にはO(n log n)、最悪ではO(n^2)
- 中間要素を選び、それより大きい部分リストと小さい部分リストを選び出し、連結する。
- Merge Sort O(n log n)
- 分割統治。リストを二つに分け、それぞれをソートし、順序の整合が取れるようにマージ。
- どんなアルゴリズムでもΩ(n log n)の時間がかかる。
(memo:データに制約をつければO(n)にもなりうる。Radix Sort)
- Linear Decision Tree
- プログラムの実行パスをツリーの形で全て書き表したもの。
葉の部分に実行結果が現れる。
Insent SortのLinear Decision Treeの高さは有限。
各比較について分岐が一つできる。
最も木の高さが高くなる最悪のパスでは、O(n^2)になる。
- 正しいソーティングアルゴリズムでは、出力になり得る組み合わせはn!通り。
木の高さをできるだけ低くして葉の数を増やすことを考えると、
(深さ)≧ceil(log[2](n!))=O(n log n)
二要素の比較だけを使ってソートするときの計算量の下限はO(n log s)
Linear Decision Treeで表したときにバランスの取れた二分木になるようなアルゴリズムが最良のソーティングアルゴリズム。
- 行列積
- A,B ∈ R^(n×n)
C = AB
c[i][j] = Σ[k=1,n]a[i][k]b[k][j]
式をそのまま計算すると、O(n^3)
これより計算量の少ない計算方法は存在するだろうか?
- 行列をうまく分割して計算するとO(n^log[2]7)≒O(n^2.807)で計算できる。Strassenのアルゴリズム
- 現在ではO(n^2.386)まで下げられている。下限はΩ(n^2)以上だとしかわかっていない。
- 漸近的性質
関数f,g:N⇒Nについて
- O
f(n) = O(g(n))⇔∃n,∃c,∀m≧n. f(m)≦c*g(m)
- Ω
f(n) = Ω(g(n))⇔∃n,∃c,∀m≧n. f(m)≧c*g(m)
- Θ
f(n) = Θ(g(n))⇔f(n)=O(g(n))∧f(n)=Ω(g(n))
- o
f(n)=o(g(n))⇔lim[n→∞]f(n)/g(n)=0
- 入力サイズnについて、アルゴリズムAの計算時間t(n)がどう増えてゆくか。
- P: t(n)がnの多項式のオーダーとなるアルゴリズムが存在する問題族
多項式オーダー:O(n^c),
n,n log(n),n^2,√n,…
- EXP:t(n)がnの指数関数のオーダーとなるアルゴリズムが存在する問題族
指数関数オーダー(singly exponential):O(2^p(n)),p(n)=O(n^c)
2^n,n!,n^n=2^(n log(n)),3^(n^2)
- P⊂EXP, nを十分に大きくすると常にEXPの問題の方が大きくなる。
EXPに属する問題は手におえないくらい計算時間が長くなる。
P:tractable 手に終える
Pより上:intractable 手に負えない
ではEXPとPの境界はどこにあるか。
それより難しい問題はどう解くか。
- 計算の難しさ。(上に行くほど難しい。)
- undecidable:計算不能、アルゴリズムが存在しない。
Turing Machineの停止問題
- decidable:計算可能、アルゴリズムが存在する。
- 多重指数オーダーで解ける。 Presburger Arithmetic
- intractable:実行不可能、多項式オーダーでは解けない。
- NP完全問題。非決定性チューリングマシンで多項式オーダーで計算できる。
境界はまだ曖昧。
TSP,SAT,coloring
- tractable:実行可能、多項式オーダーで解ける。
- アルゴリズムとは何か
- 計算とは、状態遷移だ。
- Turing Machine
有限長のプログラム(内部状態)と無限の長さの一次元記憶媒体(テープ)を持った仮想的な機械。
- TM=(Γ,Σ,Q,δ)
Γ=Σ∪{b} テープのセルに書く記号の集合。
- Σ 問題を記述する記号の集合。alphabet
- Q 機械の内部状態の集合。有限。
q[0]:初期状態
q[y]:停止状態、受理
q[n]:停止状態、非受理
- δ:Q×Γ→Q×Γ×{+1,-1} 遷移関数。現在の状態と現在地のテープの記号から、
次の時刻の状態とテープに上書きする値、テープ上の位置の変化を出す関数。
- 初期状態から、遷移関数に従ってテープ上に記録されたデータを書き換えながら
内部状態とテープ上の位置を変化させ、停止状態になるまで動き続ける。
停止状態になったらyes,noのいずれかを返す。
停止しないこともありうる。
テープ上に入力を与え、出力としてyes,noを返す計算のモデル。
- 現在のコンピュータで多項式時間で解ける問題はチューリングマシンでも多項式時間で解ける。逆も成立。
- δが一価の関数→決定性チューリングマシン
δが多価関数→非決定性チューリングマシン
- 決定性チューリングマシン(DTM,Deterministic Turing Machine)
- 通常のチューリングマシン。同じ入力に対して同じ出力を返す。遷移関数が一価関数。
- 計算資源、サイズnの入力に対して最悪の場合の量を指す。
time complexity:遷移関数を適用する回数。
space complexity:headが少なくとも一度見たセルの数。
- P:チューリングマシンでの時間計算量が、入力のサイズの多項式で押えられるアルゴリズムが存在する問題。
PSpace:空間計算量が、入力のサイズの多項式で押えられるアルゴリズムが存在する問題。
- PTime ⊂ PSpace ⊂ ExpTime
- 空間計算量がnの多項式で押えられる問題は、時間計算量はexp以下になる。
- 無限ループに陥らないアルゴリズムの実行中には、状態遷移の過程で、同じ状態になることはできない。
空間計算量が多項式で押えられると、状態遷移で通過できる状態数は指数オーダーで押えられる。
- 非決定性チューリングマシン(NTM,Nondeterministic Turing Machine)
- 同時に複数の状態をとりうる、遷移関数が多価関数になりうる拡張されたチューリングマシン。並列計算のモデル化?
- 計算資源
time complexity:NTMを次々に分岐させながらステップを進めて行き、最も早くyesを返して停止した分岐までのステップ数。
space complexity:最も早くyesを返して停止した分岐での、少なくとも一度見たセルの数。
- NP:非決定性チューリングマシンでの時間計算量が、入力サイズの多項式で押えられるアルゴリズムが存在する問題。
- PTime ⊂ NP ⊂ PSpace
- NTMをDTMでシミュレート。各ステップを幅優先探索。
バックトラックの状態復元に使うメモリは、深さが多項式オーダーなら、多項式オーダー。
- 並列計算をしたときや、計算機が速くなったときの、同一時間で解ける問題のサイズ。
- プロセッサ数がp倍になったときに、
O(n) p倍
O(n^2) √p倍
O(2^n) log p倍。
- 多項式時間変換(Polynomial-time Reducibility)
- ハミルトン閉路(HC,Hamilton Circuit)問題
入力:グラフ
出力:入力グラフがHCを持つか否か。
- 巡回セールスマン問題の判定
完全グラフ。距離関数。パラメタ一つ。
総長がパラメタの値以下のHCが存在するかどうか。
- ある問題クラスΠの、任意のインスタンスが、別のあるクラスΠ'のインスタンスに多項式時間で帰着できるなら、
ΠはΠ`に多項式時間変換可能だという。
f:Π→Π'. π:yes⇔f(π):yes
- ハミルトン閉路問題は、多項式時間で巡回セールスマン問題に多項式時間で変換可能。
完全グラフ化して、追加したグラフの重みを大きくしておく。
- NTM(Oracle版)
- Guessing Module付きのDTM
- 入力xがセル1からセル|x|まで与えられている。
「Advice」をGuessing Moduleがセル(-1)から左に書く。
Guessing Moduleを停止してDTMとして起動。処理。停止。
- NTMでどの分岐をすべきかをあらかじめ外部から与えたもの。
- NTMを使うと多項式時間で解ける問題は、DTMで多項式時間で正解を検証できる問題。
- 命題論理の充足可能性判定問題(SAT,Satisfiability)
- 入力:CNF命題論理式(CNF,Conjunctive Normal Form,∧標準形)
- 出力:入力の論理式を満たす真偽値の組み合わせがあればTrue,なければFalse
- 入力は論理変数をn個持った論理式で、論理変数と¬と∨からなる節(Clause)を∧で連ねた形に標準化されたもの。
うまく論理変数の値を選んだとき、論理式全体を真にできるとき、その論理式は充足可能。
どの組み合わせを選んでも真にできないとき、恒偽、充足不可能と呼ぶ。
- この充足可能性問題は
ここLostかも。後で補完。
- NPの中で多項式時間還元を考えることでNPを分類する。
多項式時間還元で擬順序を導き、擬順序から導かれる同値関係でNPを分割。
分割された塊の間には、多項式時間還元によって半順序が入っている。
この半順序には最小元と最大元が存在する。最小限はP、最大限はNP完全問題。
- NP完全
NP問題クラス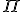 のうちで、任意のNP問題クラス
のうちで、任意のNP問題クラス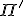 の問題を
の問題を
多項式時間で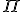 に帰着できるなら、
に帰着できるなら、
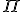 はNP完全という。
はNP完全という。
NP完全な問題のどれか一つに多項式時間アルゴリズムが存在すれば、
任意のNP問題が多項式時間で解ける。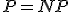
NP完全な問題には多項式時間アルゴリズムは存在せず、
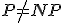 だろうという考えが大勢になっている。
だろうという考えが大勢になっている。
SAT,TSPなど、多くの問題がNP完全であることがわかっている。
- Karpのreduction
- 問題クラス&mimetx(\Pi);がNP完全であることを示したいときには、
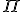 がNP問題であることと、適当なNP完全問題
がNP問題であることと、適当なNP完全問題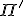 を
を
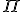 に多項式時間還元ができることを示せばいい。
に多項式時間還元ができることを示せばいい。
ではどのNP完全問題に帰着できることを示すのがよいか。
- SATはNP完全。SATを他の問題に連鎖的に帰着させてNP完全性を示す。
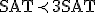
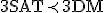
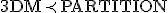
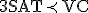
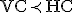
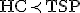
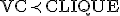
- 3SAT
入力:3-CNF論理式(各節が3つの命題からなる和積標準形の論理式)
和積標準形論理式の節は、論理積で連なっている論理和からなる塊。
出力:論理式を真にする命題の組み合わせが存在するか。
- 3SATはNP問題。SATはNP問題。3SATはSANの部分クラス。
- 任意のSATの問題を3SATに多項式時間還元できることを示せば、3SATがNP完全であることを証明できる。
任意のSATの問題の各節について、
節に含まれる論理変数の数が1,2,3のときには、新たに論理変数を追加して水増し。3変数にする。
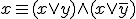
論理変数の数が4以上。例えば5のときには、
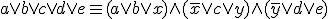 と変形すれば3変数にできる。
と変形すれば3変数にできる。
ゆえに任意のSATの問題は多項式時間で3SAT問題に帰着可能。
- cf)2SAT
入力を2-CNF論理式に限った2SATは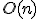 、P問題。
、P問題。
- VC(Vertex Cover)。無向グラフの被覆問題。
入力:無向グラフとパラメタK。
出力:サイズK以下のVertex Coverが存在するか否か。
- 3SAT問題をVCに帰着すれば、VCがNP完全であることを示せる。
VCはNP問題。解が与えられればそれがサイズK以下の被覆になっていることは
多項式時間で確かめられる。
3SATの論理式をグラフに変換し、充足可能性とVCの存在が同値になるようにKを選ぶ。
各論理変数とその否定を頂点とし、肯定形と否定形を頂点でつないで2点からなるグラフを作り、
各節に対応して、その論理変数に応じた三角形のグラフを作り、
節に対応するグラフの頂点と、それに対応する論理変数を繋ぐ。
Kとして、(論理変数の数)+2*(節の数)をとってVC問題とすると、
3SATをVCに帰着できる。
- Vertex Cover
任意の辺の少なくとも一方が含まれるように、グラフの頂点からいくつかを選び出す。
- cf)2部グラフについては、最小VC探索はP問題。最小VCは最大マッチングを与える。
- 先生会議中。代理の人が講義。
- PSPACE = NPSPACE
- PSPACE
決定性チューリングマシンで、入力サイズに対して領域計算量が多項式オーダーで計算可能。
- NPSPACE
非決定性チューリングマシンで、入力サイズに対して領域計算量が多項式オーダーで計算可能。
- 有向グラフの連結性判定
入力:有向グラフ。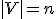
出力:頂点s,tを結ぶ長さが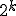 以下の路があるか否か。
以下の路があるか否か。
- STCONのアルゴリズム
長さが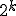 以下の有向路があるか否かを返す関数reachを使って、
以下の有向路があるか否かを返す関数reachを使って、
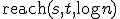 を実行すればよい。
を実行すればよい。
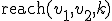
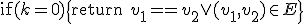
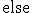
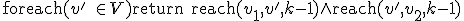
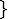
- 一回の再帰には
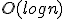 の計算領域、再帰の深さは
の計算領域、再帰の深さは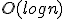 なので、
なので、
計算領域は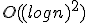 だけ必要、PSPACE。
だけ必要、PSPACE。
- PSPACE = NPSPACEの証明
PSPACE 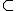 NPSPACE は定義から自明。
NPSPACE は定義から自明。
NPSPACE 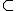 PSPACE を証明するために、
PSPACE を証明するために、
チューリングマシンのスナップショットからなるグラフを考える、
各スナップショットをノードにし、遷移規則から枝を定める。
計算領域がNTMで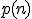 であるとすると、
頂点数は、(状態数)*(使う領域幅)*(テープの内容)^(使う領域幅)で、
であるとすると、
頂点数は、(状態数)*(使う領域幅)*(テープの内容)^(使う領域幅)で、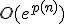
このグラフに対してTMでSTCONのアルゴリズムを走らせると、
領域計算量は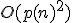 なので、TMで多項式空間計算量でシミュレート可能。
なので、TMで多項式空間計算量でシミュレート可能。
- STCONはNLOG完全。NTMでO(log(n))で計算可能。
- LOG
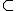 NLOG
NLOG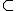 (LOG)^2
(LOG)^2
- STCONが
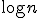 SPACEで計算可能かどうかは未解決。
SPACEで計算可能かどうかは未解決。
- Randomized Algorithmなら
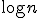 SPACEで計算可能。
SPACEで計算可能。
- 無向グラフなら
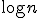 SPACEで計算可能。
SPACEで計算可能。
- NP-Completeの意義
- P
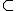 NP
NP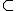 PSPACE=NPSPACE
PSPACE=NPSPACE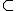 EXPTIME
EXPTIME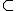 NEXPTIME
NEXPTIME
- NP完全問題が一つでもPであることがわかれば、P=NP。
任意のNP問題がPであることがわかる。
- P問題はTractable、それ以外はIntractableだと考え。
P=NPではないことを想定して、NP完全であることを示すことで、問題がIntractableであることを示す。
NP完全であることを示すことがパラダイムになっている。
- Ristriction
- NP完全な部分問題を含むNP問題は、NP完全問題。
問題を限定した上でNP完全性を示し、全体の問題クラスもNP完全であることを得る。
- 部分グラフ同型判定問題
入力:無向グラフ2つ。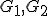
出力: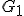 が
が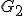 と同型な部分グラフを持つか否か。
と同型な部分グラフを持つか否か。
- CLIQUE
入力:無向グラフ。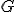
出力: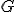 がサイズk以上の完全グラフを部分グラフを持つか。
がサイズk以上の完全グラフを部分グラフを持つか。
- 同型になる部分グラフと同型写像が与えられれば、確かめることは多項式時間で可能。NP問題。
- CLIQUEは部分グラフ同型判定問題の部分問題。
CLIQUEがNP完全ならば部分グラフ同型判定問題はNP完全。
- Local Transformation
- Component Design
- NP完全性を示す事で、問題が難しいことを示す。
問題の簡単さを示すには、多項式時間で解けるアルゴリズムを見つければよい。
- SATはNP完全問題。
3-SATもNP完全問題。
2-SATはP問題で、O(n)で解ける。
SATは節の中の論理変数の数で階層化できる。
k-SATは、k=2ではP問題。k≧3ではNP完全問題。
同様な階層化はk部グラフのマッチング問題でもできる。
- HORN
SATの部分問題。各節に正リテラルが高々1つ。P問題。O(n)で解ける。
- 難しさの異なる似た問題をNP完全か、Pかで類別する。
- 枝長非負なグラフの最短路問題はP問題。(Dijkstra法)
- 最長単純路問題はNP問題。
単純路:同じ頂点を2度は通らない路。
- 有向閉路のないグラフでの最長路問題はP問題。(DFS,topological sort)
- グラフの最小点被覆
点による枝の被覆。NP完全問題。
グラフからいくつか点を選び出し、各枝について
その枝の端点のどちらかは選ばれるようにする。
選ばれる点数はできるだけ少なくする。
2部グラフの点被覆を求めるのはP問題。
- グラフの最小枝被覆
枝による点の被覆。P問題。
グラフから枝をいくつか選び出し、全ての点について
その点につながる枝のどれかは選ばれているようにする。
選ばれる枝数はできるだけ少なくする。
- 最小切断
点集合を2つに分け、その間をまたぐ枝数をできるだけ少なくする。
P問題。
- 最大切断
点集合を2つに分け、その間をまたぐ枝数をできるだけ多くする。
NP完全問題。
平面グラフの限定すればP問題。
- グラフの次数に着目。
点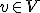 について、
について、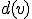 は、
は、 に接続する枝の数。
に接続する枝の数。
グラフの次数は、各点の次数の最大値。
Vertex Cover、Hamilton circuitなどは、次数2以下のグラフについてはP問題。それを超えるとNP完全。
- 数系のNP完全問題
- PARTITION
入力:n個の整数。
出力:入力を2分割して、それぞれの和を等しくできるか否か。
- 困難さ
分割の仕方は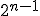 。
。
整数の大きさに制限がない。
- 動的計画法(DP,Dynamic Programming)
- 全体での最適な構造が、部分的にも最適な構造になっている。
- Shortest Path
階層化された有向グラフ上での最短経路を求める。
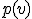 を始点から
を始点から への最短路長とすると、
への最短路長とすると、
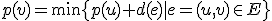
始点からある層の各点への最短路の値から、次の層の各点への始点からの最短路を求められる。
- PARTITION
入力:n個の正整数
出力:その和が等しくなるように入力された整数を
二つのグループに分割することができるか否か。
- DPで解く
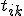 を、
を、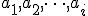 の部分集合で、
の部分集合で、
和が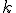 のものが存在すればTrue,存在しなければFalse。と定義すれば、
のものが存在すればTrue,存在しなければFalse。と定義すれば、
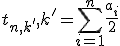 が解。
が解。
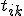 は
は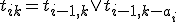 を満たすので
を満たすので
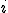 について次々に計算できる。
について次々に計算できる。
時間計算量は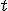 のテーブルの大きさ分、
のテーブルの大きさ分、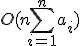 で解ける。
で解ける。
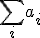 の大きさがnの多項式で押さえられるならば、多項式時間で解ける。
の大きさがnの多項式で押さえられるならば、多項式時間で解ける。
入力長は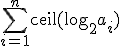 ほど、
ほど、
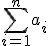 は入力長に対して指数オーダー。
は入力長に対して指数オーダー。
- Number Problem
数がからむ問題では、入力長に対し、数がとても大きくなりうることが難しさのポイント。
問題の構成要素の個数と独立な値になっている。
問題のインスタンス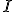 の入力長を
の入力長を![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif)
現れる数の最大値を![\mathrm{Max}[I]](./cache/5dc52557113755b5aeddeedacef72382.mimetex.gif) とすると、
とすると、
PARTITIONは![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif) に対して多項式時間。
に対して多項式時間。
これを擬多項式時間アルゴリズム(pseudo-polynomial)と呼ぶ。
P問題は![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif) について多項式時間でなければならない。
について多項式時間でなければならない。
PARTITIONは擬多項式時間アルゴリズムは存在するが、NP完全なので
真の多項式時間アルゴリズムはおそらく存在しない。
- 任意のNP完全な問題に擬多項式時間アルゴリズムは存在するか?
NP完全問題をさらに分割できる。
- Strong NP-Complete
NP完全問題で、![\mathrm{Max}[I]=O(\mathrm{poly}(\mathrm{Length}[I]))](./cache/713eba8566035adc9228fb52d66aea21.mimetex.gif) の場合でもNP完全のとき、
の場合でもNP完全のとき、
その問題は強NP完全問題と呼ぶ。
(P≠NPの仮定のもと、)強NP完全は擬多項式時間アルゴリズムを持たない。
- 計算問題
ここまで扱ってきたのは受理問題。戻り値はyes,no。
計算問題や探索問題について難しさの尺度を与えられないか。
Turing還元のもとで問題クラスを分類する。//と、NP困難(NP-hard)が現れる。
- Search Problem
探索問題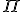 とは、
とは、
インスタンスの集合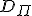 で、
で、
各インスタンス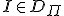 に対して
に対して
解![S_{\Pi}[I]](./cache/808e087697fad6fadd80485d18cc095e.mimetex.gif) が存在。
が存在。
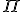 を解くアルゴリズムとは、
を解くアルゴリズムとは、
![S_{\Pi}[I]=\phi](./cache/9558f24ad0c7fd6fb0eaeb6d485ecfd0.mimetex.gif) のとき、"no"と答え、
のとき、"no"と答え、
そうでないとき、![S_{\Pi}[I]](./cache/808e087697fad6fadd80485d18cc095e.mimetex.gif) の要素を1つ出力するアルゴリズム。
の要素を1つ出力するアルゴリズム。
- Poly-time Turing Reduction
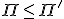
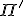 を単位時間で解くサブルーチンを使っていいときに、
を単位時間で解くサブルーチンを使っていいときに、
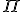 を多項式時間で解くアルゴリズムが存在すること。
を多項式時間で解くアルゴリズムが存在すること。
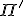 が多項式時間で解けるならば、
が多項式時間で解けるならば、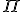 も多項式時間で解ける。
も多項式時間で解ける。
- NP困難(NP-hard)
NP完全な問題にTuring Reductionできる問題クラスをNP困難な問題と呼ぶ。
NPなNP困難問題はNP完全問題。
TSP判定版はNP完全。TSP探索版はNP困難。
- Coping with NP-Complete Problems
NP完全問題は難しい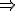 近似的に解く。
近似的に解く。
Poly-timeでできるだけいい近似解を探す。
Poly-timeで高い確率で厳密解を探す。
- bin-packing
一次元の引越しトラック最小化問題、NP困難。
n個の品物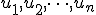
品物のサイズ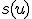 、
、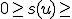
容量1のビンいくつかに品物を詰めて行き、ビンの数を最小化する。
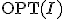 を最適解
を最適解
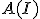 をアルゴリズム
をアルゴリズム による解。
による解。
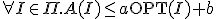 となるアルゴリズム
となるアルゴリズム を
を
この問題の近似アルゴリズムと呼ぶ。 は近似値比と呼ぶ。
は近似値比と呼ぶ。
- 単純な方法
FF(First Fit)
ビンを十分多く準備しておき、各品物について
ビンを左から見ていき、最初に詰められるビンに詰めて行く。
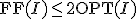 の近似アルゴリズム
の近似アルゴリズム
- この証明のためには、
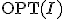 の値を何らかの形で評価する必要がある。
の値を何らかの形で評価する必要がある。
「液体版」bin-packingの解で下から抑えられる。
オレンジジュースとコーヒーと味噌汁とコーンポタージュを
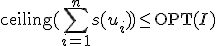
FFでは半分以下しか入っていないビンは高々1つ。
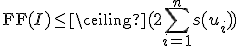
- 実際は、
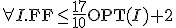
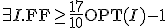 が成立。
が成立。
近似値比は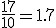
- FFD(First Fit Decreasing)
まず品物を降順にソートしてからFFで詰める。
FFDだと、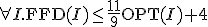
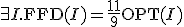 が成立。
が成立。
近似値比は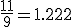
worst-caseでFFよりもFFDの方が優れていると、定量的に言えた。
- 任意の正数
 について、近似値比
について、近似値比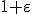 が達成できる場合と、
が達成できる場合と、
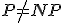 の仮定のもと、
の仮定のもと、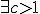 、近似値比
、近似値比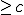 となる場合がある。
となる場合がある。
bin-packingは前者。TSPは後者。
- 近似アルゴリズム
- Metric TSP
完全グラフと距離関数の形で問題が与えられたTSP。
距離関数は三角不等式を満たす。2点間の最短距離は直に2点をつないだもの。
NP困難。近似値比2の近似アルゴリズムが存在する。
- Euclidean TSP
2次元平面上にn点が与えられ、距離がユークリッド距離のMetric TSP。
まだNP困難。
- MST(Minimum Spanning Tree)近似
- グラフの最小木
 を求め、その各枝を2重化したものを
を求め、その各枝を2重化したものを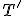 とする。
とする。
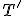 のEuler閉路を求め、閉路を順に巡る。2回目以降では点をスキップ。
のEuler閉路を求め、閉路を順に巡る。2回目以降では点をスキップ。
Metric TSPの最適解はハミルトン閉路、枝を一つ除けば木になっている。
最小木は部分木の中でもっとも短いものなので、( の長さ)
の長さ)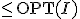
枝を2重化すると、(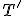 の長さ)
の長さ)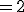 (\mimetex(T);の長さ)
(\mimetex(T);の長さ)
MST近似ではいくつか点をスキップし、Metric TSPでは点をスキップすると全長は短くなるので、
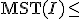 (
(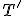 の長さ)
の長さ)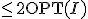
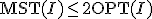 、近似値比2のアルゴリズム。
、近似値比2のアルゴリズム。
- Euler閉路:各枝を一度ずつ通る閉路。各頂点の次数が偶数なら存在する。
- MM(Min-weight Matching)近似
- グラフの最小木
 を求め、奇数次数点間の最小重み完全マッチング
を求め、奇数次数点間の最小重み完全マッチング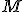 を求める。
を求める。
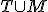 のEuler閉路を求める。後はMSTと同じ。
のEuler閉路を求める。後はMSTと同じ。
( の長さ)
の長さ)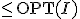
(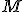 の長さ)
の長さ)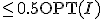
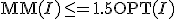
- 最小重み完全マッチング
辺の集合から、すべての点を覆うようにいくつかを選び、
枝の重みの和を最小化する。
- NN(Nearest Neighbor)
未到達の点の中で、最も近い点を訪問する。
全点に到達していたら、始点に戻って終了。
Metric TSPでは、
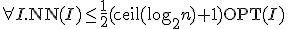
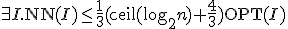
- plannar Euclidean TSP
PTASが存在する。
- PTAS
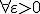 に対して、
に対して、
近似値比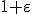 の多項式時間近似アルゴリズム。
の多項式時間近似アルゴリズム。
- Metric TSP
近似値比1.5の多項式時間近似アルゴリズムが存在する。
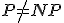 の仮定のもと、PTASは存在しない。
の仮定のもと、PTASは存在しない。
- 一般のTSP
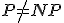 の仮定のもと、
の仮定のもと、
定数近似値比の多項式時間近似アルゴリズムは存在しない。
理学部の講義は1/10かららしいので、今日はおまけ講義
- 最長片道切符
Hamilton Pathがないネットワークで、
できるだけ総長の長い単純パスを求める。
- Hamilton Pathのないネットワークで、
各点を少なくとも一度訪れるパスで、最短のものを求める。
- 入力:有向グラフ
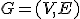
各枝の枝長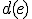 、負の有向閉路はない。
、負の有向閉路はない。
- 出力:各点を少なくとも一度訪れる最短パス。
- 通常のTSPに帰着する。
有向完全グラフ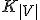 を用意し、
を用意し、
枝長を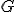 上での最短経路長に設定する。
上での最短経路長に設定する。
各点を少なくとも一度訪れる最短ルートは、
有向完全グラフ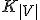 上で各点をちょうど一度ずつ訪れる最短パスになっている。
上で各点をちょうど一度ずつ訪れる最短パスになっている。
- 試験問題にしようと思っていた問題。
有向グラフ上での今の問題を解きたい。
この問題がNP-hardであることを示せ。TSPがNP-hardであることは仮定してよい。
多項式時間近似アルゴリズムで、近似値比1.5のものを与えよ。
- 「有向」だととても困難。無向にしてMetric TSPにすればできる。
- Chinese Postman
全路線を最短の長さで巡りたい。
無向グラフ上のすべての枝を少なくとも一度通る閉路のうち、総長が最短のものを求めよ。
これはP問題。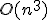 のアルゴリズムが存在する。
のアルゴリズムが存在する。
- 奇数次の点のみからなる完全グラフで、各枝の枝長が元のグラフの最短路長となるものを用意する。
その完全グラフ上で、総長最小の完全マッチングを求める。
マッチングで得られた枝を元のグラフに付け加えて、元のグラフをオイラーグラフにする。
このオイラーグラフ上でオイラーグラフを求めれば、それが最適解。
- TSPの近似可能性
- MetricTSPには近似値比1.5の近似アルゴリズムが存在する。
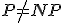 の仮定のもと、一般のTSPには、
の仮定のもと、一般のTSPには、
定数近似値比の多項式時間近似アルゴリズムは存在しない。
もし存在するなら、それを使ってHCを多項式時間で解けてしまう。
HCがあるかどうかを判定すべきグラフに、枝を追加し、完全グラフにする。
元からあった枝には重み1を、追加した枝には充分大きな重みを割り当てる。
このグラフについてTSPの近似アルゴリズムを使って、
枝長nのHCがあると判定されたらもとのグラフにもHCが存在し、
充分大きな値のHCが最短HCならもとのグラフにHCは存在しない。- Euclidian TSP
任意の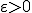 に対して、近似値比
に対して、近似値比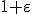 のアルゴリズムが存在する。
のアルゴリズムが存在する。
PTAS(Polynomial Time Approximation Scheme)
FPTAS(Fully PTAS)、PTASで、timeが入力長と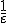 の多項式とした場合。
の多項式とした場合。
- Knapsack問題
n個の品物について、サイズ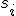 、利得度
、利得度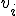 が与えられている。
が与えられている。
サイズの和が容量B以下で、利得度を最大にする組み合わせを探索する。
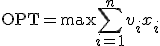
s.t 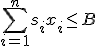 、
、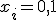
- 緩和問題
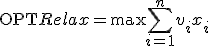
s.t 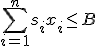 、
、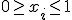
緩和問題の解は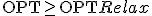
緩和問題で最適値が0,1なら、もとの問題の最適解。
うまくしらみつぶしに調べる。Branch-and-Bound
- 緩和問題はGreedyに解ける。
- PTAS
Partial Enumeration
- パラメタkについて、個数k以下の部分集合を列挙。
各部分集合について、Greedyに最適なものを探す。
- 最適な入れかたについて、
最適な品物数がk個以下の時には、最適解が見つかる。
k+1の時には、利得度が大きい順にk個まで
- Knapsack問題、Partial Enumeration
1または2の場合を試験問題として出すかも。
- FPTAS
Knapsackの単純なPTASは近似値比は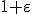 で、計算時間は&mimetex(O(n^{1+\frac{1}{\varepsilon}}\
));
で、計算時間は&mimetex(O(n^{1+\frac{1}{\varepsilon}}\
));
FPTAS、近似値比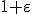 で、計算時間を入力長と
で、計算時間を入力長と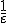 の多項式にする\\
。
の多項式にする\\
。
- Scaling + Pseudo-Poly-Time
Knapsack問題のPseudo-Poly-Timeアルゴリズムで、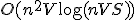
V:品物の利得度の最大値。S:品物のサイズの最大値。
利得度について動的計画法
利得度を小さく変換すれば真の多項式時間で計算できる。
- 原問題
品物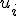
利得度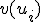
サイズ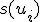
- スケール変えて粗視化する。
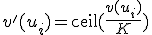
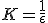 ととれば、擬多項式時間アルゴリズムが
近似値比
ととれば、擬多項式時間アルゴリズムが
近似値比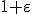 で、計算時間
で、計算時間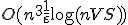 の
多項式時間近似アルゴリズムになる。
の
多項式時間近似アルゴリズムになる。
- 列挙問題
与えられた問題の解を全て重複無く見つけ出す問題、パスの列挙、クリークの列挙など。
問題の構造を把握する上で有効な手法。
解の数が膨大になることがある。すべての解の列挙ではなく、列挙する対象を選ぶことが大事。
全てのクリークではなく、極大なクリークの列挙をする。
全てのパスではなく、最短パスを列挙する。
- グラフのクリーク列挙。
完全部分グラフを列挙する。
最大クリークを求める問題はNP-Complete
極大クリークを求める問題は多項式時間でできる。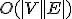
- クリークの単調性
クリークの点部分集合から誘導されるグラフはクリーク。
1点集合から始めて、集合に点を順番に追加していき、クリークにならなくなるまで点を追加する。
クリークでなくなる直前が極大クリーク。
頂点に番号をつけておくと、クリークに辞書式順序が入る。
極大クリーク から、番号が大きい順に一つずつ点を除いていった部分クリーク
から、番号が大きい順に一つずつ点を除いていった部分クリーク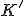 について、
について、
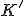 を含むクリークで、辞書式順序最小のものが
を含むクリークで、辞書式順序最小のものが でないときに、それを
でないときに、それを の親と呼ぶ\\
。
の親と呼ぶ\\
。
この親子関係で木を作り、深さ優先探索をすれば、クリークを重複無く全て列挙することができる。
非巡回的な親子関係と、子供を見つける多項式時間アルゴリズムがあれば、多項式時間列挙ができる。
- 子供候補の見つけかた
クリーク に隣接する頂点
に隣接する頂点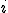 と頂点
と頂点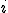 に隣接する頂点からなるクリークを含む
に隣接する頂点からなるクリークを含む
辞書式さ衣装のクリークを![K[i]](./cache/b3f6e41be1771f565daa27cc609d0348.mimetex.gif) とする。
とする。
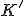 が
が の子供ならば、
の子供ならば、![K[i]=K'](./cache/3acc4dfcc34e3a635a0f4d802e57a477.mimetex.gif) がいずれかのiについて成り立つ。
がいずれかのiについて成り立つ。
子供ノードの候補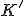 と
と の親子チェックをして、子ノードを確定する。
の親子チェックをして、子ノードを確定する。
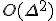 最大次数の2乗の時間で親を計算できる。探索対象は多くとも
最大次数の2乗の時間で親を計算できる。探索対象は多くとも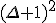 、
、
列挙一つあたりで最大次数の4乗のオーダーで求められる。
列挙については、列挙にかかった総時間ではなく、一つあたりにかかった時間が多項式時間かどうかが問題となる。
列挙対象が指数オーダーになることもあるので総時間での多項式性はあきらめる。(多項式時間遅延)
- 近似は難しさに対抗する手段。
近似の性能の評価は近似値比だけ?
- グラフの枝彩色
グラフの枝を塗り分ける。同じ点に接続する枝は違う色にする。
点彩色と同様にNP完全。
2部グラフの枝彩色なら多項式時間アルゴリズムが存在する。
n次完全2部グラフの彩色はn色でできる。
全点の次数がkの2部グラフの彩色はk色でできる。
- 最大次数kの2部グラフの枝グラフは、k色で彩色可能。多項式時間で彩色できる。
- 最大次数kの一般のグラフは、k色で彩色可能か、もしくは(k+1)色で彩色可能。
この判定はNP-Complete。(k+1)色で塗るのは多項式時間で可能。
解の比ではなく、解の差に越えがたい壁がある。
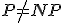 の仮定のもと、多項式時間で定数差近似ができない問題が存在する。
の仮定のもと、多項式時間で定数差近似ができない問題が存在する。
グラフの最大安定集合、クリーク、枝彩色問題
基本的な証明技法は背理法。定数差近似kが存在したら、グラフを(k+1)個にコピーした問題を解けば、
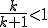 、差の絶対値が1未満の2整数は等しい。
、差の絶対値が1未満の2整数は等しい。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
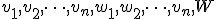
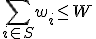 を満たし
を満たし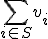 を最大化するような
を最大化するような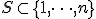 を求める.
を求める.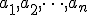
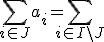 なる
なる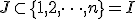 は存在するか?
は存在するか?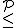 3SAT
3SAT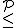 3DM
3DM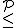 PARTITION
と示せる.
PARTITION
と示せる.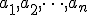 が与えられたとき,
が与えられたとき,
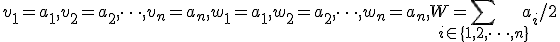 とする.
とする.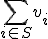 の最大値が
の最大値が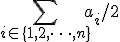 であるかどうかが分かればPARTITION問題が解ける.
であるかどうかが分かればPARTITION問題が解ける.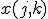 を
を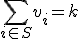 となるものの中での
となるものの中での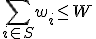 の最小値とする.ただし
の最小値とする.ただし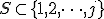 とする.
とする.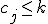 かつ
かつ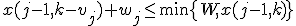 のときは
のときは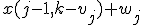 ,
それ以外のときは
,
それ以外のときは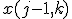 を埋めていく.
を埋めていく.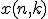 を走査すれば,何が選ばれたのかが分かる.
を走査すれば,何が選ばれたのかが分かる.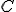 を最適解の値の上界として
を最適解の値の上界として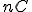 .
例えば
.
例えば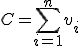 とできるが,これは擬多項式時間アルゴリズムである.
とできるが,これは擬多項式時間アルゴリズムである.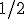 近似アルゴリズム.
近似アルゴリズム.
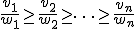
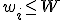 を満たすものを取り出し,
を満たすものを取り出し,
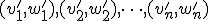
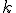 を
を
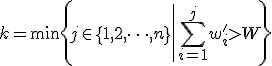
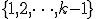 と
と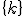 のうち
より良い方の解を選ぶ.(どちらも実行可能解であることに注意.)
のうち
より良い方の解を選ぶ.(どちらも実行可能解であることに注意.)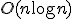 ,条件を満たす
,条件を満たす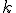 を求めるために
を求めるために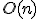 かかるので,合わせて
かかるので,合わせて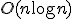 である.
多項式時間.
である.
多項式時間.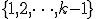 と
と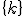 の二つの解の和は明らかに最適解以上のものとなっているので,近似値比は
の二つの解の和は明らかに最適解以上のものとなっているので,近似値比は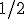 である.
である.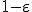 近似値比アルゴリズムが存在することを示せばよい.
近似値比アルゴリズムが存在することを示せばよい.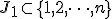 とする.
とする. に対して,
に対して,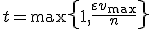 と置く.
と置く.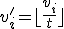 と修正したinstanceについて
と修正したinstanceについて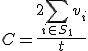 動的計画法を用いて得られる解を
動的計画法を用いて得られる解を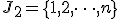 とする.
とする.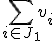 と
と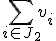 を比べ,大きいほうを出力する.また,その解を
を比べ,大きいほうを出力する.また,その解を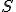 とする.
とする.
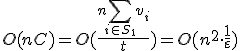 .
.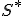 と書くことにすると,
と書くことにすると,
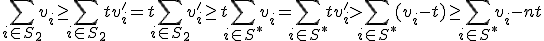
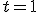 のときは,
のときは,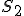 は最適解であり,そうでないときは上の不等式より
は最適解であり,そうでないときは上の不等式より
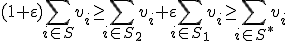
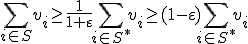 となるので
となるので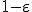 近似値比である.
近似値比である.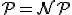 でない限り,KNAPSACK問題には,最適解と高々定数差しかない近似解を求める多項式時間アルゴリズムが存在しない.
でない限り,KNAPSACK問題には,最適解と高々定数差しかない近似解を求める多項式時間アルゴリズムが存在しない.
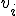 すべてに,十分大きい定数を掛けると近似解が最適解となるので
すべてに,十分大きい定数を掛けると近似解が最適解となるので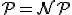 となる.
となる.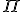 のうちで、任意のNP問題クラス
のうちで、任意のNP問題クラス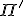 の問題を
の問題を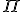 に帰着できるなら、
に帰着できるなら、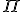 はNP完全という。
はNP完全という。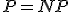
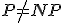 だろうという考えが大勢になっている。
だろうという考えが大勢になっている。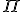 がNP問題であることと、適当なNP完全問題
がNP問題であることと、適当なNP完全問題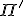 を
を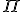 に多項式時間還元ができることを示せばいい。
に多項式時間還元ができることを示せばいい。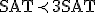
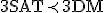
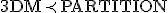
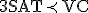
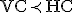
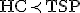
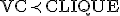
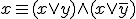
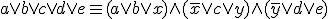 と変形すれば3変数にできる。
と変形すれば3変数にできる。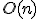 、P問題。
、P問題。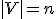
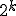 以下の路があるか否か。
以下の路があるか否か。
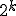 以下の有向路があるか否かを返す関数reachを使って、
以下の有向路があるか否かを返す関数reachを使って、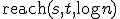 を実行すればよい。
を実行すればよい。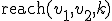
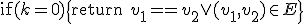
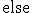
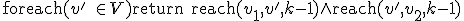
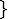
 の計算領域、再帰の深さは
の計算領域、再帰の深さは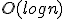 なので、
なので、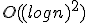 だけ必要、PSPACE。
だけ必要、PSPACE。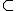 NPSPACE は定義から自明。
NPSPACE は定義から自明。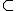 PSPACE を証明するために、
PSPACE を証明するために、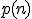 であるとすると、
頂点数は、(状態数)*(使う領域幅)*(テープの内容)^(使う領域幅)で、
であるとすると、
頂点数は、(状態数)*(使う領域幅)*(テープの内容)^(使う領域幅)で、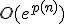
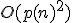 なので、TMで多項式空間計算量でシミュレート可能。
なので、TMで多項式空間計算量でシミュレート可能。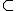 NLOG
NLOG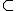 (LOG)^2
(LOG)^2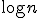 SPACEで計算可能かどうかは未解決。
SPACEで計算可能かどうかは未解決。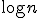 SPACEで計算可能。
SPACEで計算可能。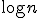 SPACEで計算可能。
SPACEで計算可能。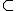 NP
NP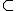 PSPACE=NPSPACE
PSPACE=NPSPACE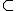 EXPTIME
EXPTIME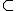 NEXPTIME
NEXPTIME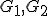
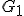 が
が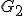 と同型な部分グラフを持つか否か。
と同型な部分グラフを持つか否か。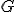
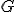 がサイズk以上の完全グラフを部分グラフを持つか。
がサイズk以上の完全グラフを部分グラフを持つか。
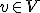 について、
について、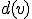 は、
は、 に接続する枝の数。
に接続する枝の数。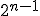 。
。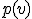 を始点から
を始点から への最短路長とすると、
への最短路長とすると、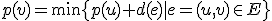
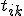 を、
を、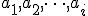 の部分集合で、
の部分集合で、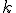 のものが存在すればTrue,存在しなければFalse。と定義すれば、
のものが存在すればTrue,存在しなければFalse。と定義すれば、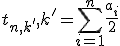 が解。
が解。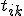 は
は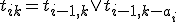 を満たすので
を満たすので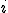 について次々に計算できる。
について次々に計算できる。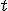 のテーブルの大きさ分、
のテーブルの大きさ分、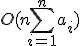 で解ける。
で解ける。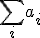 の大きさがnの多項式で押さえられるならば、多項式時間で解ける。
の大きさがnの多項式で押さえられるならば、多項式時間で解ける。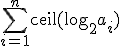 ほど、
ほど、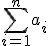 は入力長に対して指数オーダー。
は入力長に対して指数オーダー。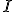 の入力長を
の入力長を![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif)
![\mathrm{Max}[I]](./cache/5dc52557113755b5aeddeedacef72382.mimetex.gif) とすると、
とすると、![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif) に対して多項式時間。
に対して多項式時間。![\mathrm{Length}[I]](./cache/992aeb1832fbcf7eedc0e1f8c8e95b0a.mimetex.gif) について多項式時間でなければならない。
について多項式時間でなければならない。![\mathrm{Max}[I]=O(\mathrm{poly}(\mathrm{Length}[I]))](./cache/713eba8566035adc9228fb52d66aea21.mimetex.gif) の場合でもNP完全のとき、
の場合でもNP完全のとき、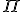 とは、
とは、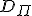 で、
で、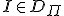 に対して
に対して![S_{\Pi}[I]](./cache/808e087697fad6fadd80485d18cc095e.mimetex.gif) が存在。
が存在。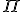 を解くアルゴリズムとは、
を解くアルゴリズムとは、![S_{\Pi}[I]=\phi](./cache/9558f24ad0c7fd6fb0eaeb6d485ecfd0.mimetex.gif) のとき、"no"と答え、
のとき、"no"と答え、![S_{\Pi}[I]](./cache/808e087697fad6fadd80485d18cc095e.mimetex.gif) の要素を1つ出力するアルゴリズム。
の要素を1つ出力するアルゴリズム。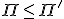
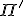 を単位時間で解くサブルーチンを使っていいときに、
を単位時間で解くサブルーチンを使っていいときに、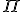 を多項式時間で解くアルゴリズムが存在すること。
を多項式時間で解くアルゴリズムが存在すること。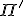 が多項式時間で解けるならば、
が多項式時間で解けるならば、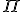 も多項式時間で解ける。
も多項式時間で解ける。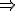 近似的に解く。
近似的に解く。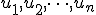
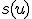 、
、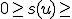
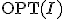 を最適解
を最適解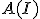 をアルゴリズム
をアルゴリズム による解。
による解。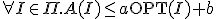 となるアルゴリズム
となるアルゴリズム を
を は近似値比と呼ぶ。
は近似値比と呼ぶ。
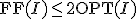 の近似アルゴリズム
の近似アルゴリズム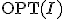 の値を何らかの形で評価する必要がある。
の値を何らかの形で評価する必要がある。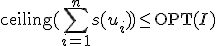
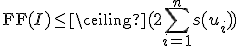
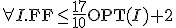
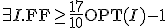 が成立。
が成立。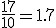
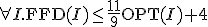
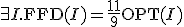 が成立。
が成立。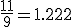
 について、近似値比
について、近似値比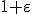 が達成できる場合と、
が達成できる場合と、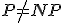 の仮定のもと、
の仮定のもと、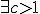 、近似値比
、近似値比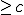 となる場合がある。
となる場合がある。 を求め、その各枝を2重化したものを
を求め、その各枝を2重化したものを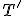 とする。
とする。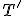 のEuler閉路を求め、閉路を順に巡る。2回目以降では点をスキップ。
のEuler閉路を求め、閉路を順に巡る。2回目以降では点をスキップ。 の長さ)
の長さ)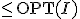
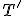 の長さ)
の長さ)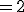 (\mimetex(T);の長さ)
(\mimetex(T);の長さ)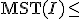 (
(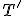 の長さ)
の長さ)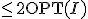
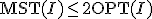 、近似値比2のアルゴリズム。
、近似値比2のアルゴリズム。
 を求め、奇数次数点間の最小重み完全マッチング
を求め、奇数次数点間の最小重み完全マッチング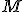 を求める。
を求める。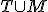 のEuler閉路を求める。後はMSTと同じ。
のEuler閉路を求める。後はMSTと同じ。 の長さ)
の長さ)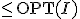
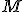 の長さ)
の長さ)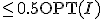
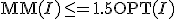
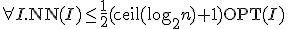
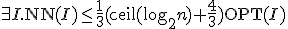
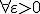 に対して、
に対して、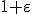 の多項式時間近似アルゴリズム。
の多項式時間近似アルゴリズム。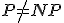 の仮定のもと、PTASは存在しない。
の仮定のもと、PTASは存在しない。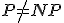 の仮定のもと、
の仮定のもと、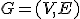
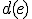 、負の有向閉路はない。
、負の有向閉路はない。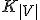 を用意し、
を用意し、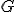 上での最短経路長に設定する。
上での最短経路長に設定する。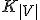 上で各点をちょうど一度ずつ訪れる最短パスになっている。
上で各点をちょうど一度ずつ訪れる最短パスになっている。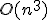 のアルゴリズムが存在する。
のアルゴリズムが存在する。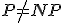 の仮定のもと、一般のTSPには、
の仮定のもと、一般のTSPには、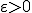 に対して、近似値比
に対して、近似値比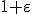 のアルゴリズムが存在する。
のアルゴリズムが存在する。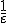 の多項式とした場合。
の多項式とした場合。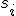 、利得度
、利得度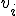 が与えられている。
が与えられている。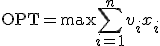
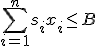 、
、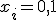
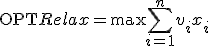
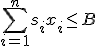 、
、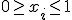
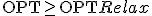
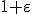 で、計算時間は&mimetex(O(n^{1+\frac{1}{\varepsilon}}\
));
で、計算時間は&mimetex(O(n^{1+\frac{1}{\varepsilon}}\
));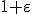 で、計算時間を入力長と
で、計算時間を入力長と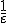 の多項式にする\\
。
の多項式にする\\
。
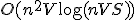
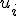
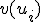
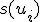
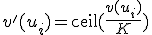
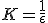 ととれば、擬多項式時間アルゴリズムが
近似値比
ととれば、擬多項式時間アルゴリズムが
近似値比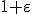 で、計算時間
で、計算時間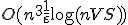 の
多項式時間近似アルゴリズムになる。
の
多項式時間近似アルゴリズムになる。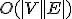
 から、番号が大きい順に一つずつ点を除いていった部分クリーク
から、番号が大きい順に一つずつ点を除いていった部分クリーク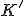 について、
について、
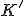 を含むクリークで、辞書式順序最小のものが
を含むクリークで、辞書式順序最小のものが でないときに、それを
でないときに、それを の親と呼ぶ\\
。
の親と呼ぶ\\
。 に隣接する頂点
に隣接する頂点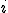 と頂点
と頂点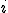 に隣接する頂点からなるクリークを含む
に隣接する頂点からなるクリークを含む![K[i]](./cache/b3f6e41be1771f565daa27cc609d0348.mimetex.gif) とする。
とする。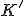 が
が の子供ならば、
の子供ならば、![K[i]=K'](./cache/3acc4dfcc34e3a635a0f4d802e57a477.mimetex.gif) がいずれかのiについて成り立つ。
がいずれかのiについて成り立つ。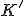 と
と の親子チェックをして、子ノードを確定する。
の親子チェックをして、子ノードを確定する。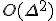 最大次数の2乗の時間で親を計算できる。探索対象は多くとも
最大次数の2乗の時間で親を計算できる。探索対象は多くとも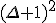 、
、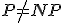 の仮定のもと、多項式時間で定数差近似ができない問題が存在する。
の仮定のもと、多項式時間で定数差近似ができない問題が存在する。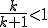 、差の絶対値が1未満の2整数は等しい。
、差の絶対値が1未満の2整数は等しい。