制御論第二 †
- 担当:津村 幸治 准教授
- 1.5単位
- 10:15-11:45 工学部六号館 63講義室
- 教科書
内容 †
- 序論
- 古典制御理論から現代制御理論へ
- 古典制御理論:(19世紀後半~1930年代)
マクスウェルによるガバナーの解析。蒸気機関の制御。
ラウス・フルビッツの安定判別法。
伝達関数によるシステムの表現。
周波数領域。ナイキストの安定判別。
時間領域。PID制御。
ウィナーフィルタ。
- 古典制御の利点
実験的に得やすい入出力特性に基づいて解析・設計する。
計算量は少ない。
直感的
- 古典制御の欠点
複雑なシステムの設計には向かない。
システムの内部状態を無視している。
方法論としての工学。理論よりも実践が優先。
- シャノンの情報理論(1948年)
「通信」の一般化
情報量と通信容量の関係。
情報量についての普遍的法則を発見。
モデルや表現法に依存しない一般法則。
- カルマンの最終目標
制御に関する純粋理論
望ましい制御を実現するためにはどのような、そしてどれくらいの情報が必要であるか?
与えられたプラントを、制御という観点から完全に特徴付ける本質的な特徴は何か?
- カルマン(1959年~1960年代)
制御問題の本質を明らかにすること。
内部状態変数。
可制御性・可観測性。
状態推定とフィードバック制御
- 動的システムと状態方程式
- 動的システム
- 粘性抵抗とダンパのシステム。~~c dx/dt = u(t)~~dx/dt = u(t)/c = f(u(t))~~ある時点でのシステムの状態は、初期状態と入力の履歴で定まる。~~x = (1/c)∫[0,t]u(τ)dτ + x(0)~~力 u(t) を入力、位置 x(t) を出力とするシステムと見なせる。
- 動的システム(Dynamical System)~~入力と出力のあるシステムで、初期状態と入力の履歴により、任意の時刻の状態が定まるもの。
- 静的システム(Static System)~~入力と出力のあるシステムで、その時刻での入力だけからその時刻の出力が定まるもの。~~内部状態のないシステム。
- 因果性(Causality)~~ある時刻の出力が、それより過去の入力のと初期状態のみによって定まること。~~出力が未来の入力に依存しないこと。~~ある時点から先の入力をカットしても、それ以前の出力はカットしないときと同じになること。~~物理的なシステムは全て因果的。音声フィルタなど、因果的でないシステムも作り得る。
- 状態方程式
- マス・バネ・ダンパー系。~~運動方程式:{M(d/dt)^2 + c(d/dt) + k}x(t) = u(t)~~出力方程式:y(t) = x(t)~~内部状態の次元を増やして、運動方程式を一階微分にする。~~ x = (x[1],x[2]) = (x,dx/dt)~~ (d/dt)x[1] = x[2]~~ (d/dt)x[2] = (u-cx[2]-kx[1])/M~~y = x[1]~~と変形すると。~~x = f(x,u)~~ y=g(x,u) の形で表せる。
- システムの状態方程式表示~~入力:u(t)~~出力:y(t)~~状態変数:x(t)を使って、~~状態方程式:dx/dt = f(x,u,t)~~出力方程式:y = g(x,u,t)の形でシステムを記述する。~~入力・出力・状態変数は多次元になりうる。~~入出力が共に一次元のシステムを、一入出力システム(SISO System)~~入出力が多次元のシステムを、多入出力システム(MIMO System)と呼ぶ。
- 線形時不変システム
- 十分長い時間、入出力が共に0となっているとする。~~動的システムP:y(t)=P[u(t)]について、~~任意の入出力関係 y_1 = P[u_1], y_2 = P[u_2] の間に、~~線形性:αy_1 + βy_2 = P[αu_1+βu_2]が成り立つとき、~~Pは線形であるという。~~状態方程式・出力方程式が線形。
- システムが任意の時間シフトについて~~y(t+τ) = P[u(t+τ)]となるとき、~~Pは時不変であるという。~~状態方程式・出力方程式に陽にtを含まない。
- 例)dx/dt = ax + u, y = x~~y = ∫[-∞,t]exp(a(t-τ))u(τ)dτ は線形時不変システム。~~t→t+t'と時間をずらすと、~~y(t+t') = ∫[-∞,t+t']exp(a(t+t'-τ))u(τ)dτ = ∫[-∞,t]exp(a(t-τ))u(τ+t')dτ
- システムが y(t) = ∫[-∞,t]p(t-τ)u(τ)dτ と、たたみこみの形で書かれていれば線形時不変システム。
- 伝達関数
- t<0でx(t)=0、∫[0,∞]|x(t)|e^(-at)dt<∞となる滑らかな関数はラプラス変換でき、~~x(t)→X(s)=∫[0,∞]x(t)exp(-st)dt と表す。~~逆変換も存在し、x(t)=(1/(2πi))∫[c-i∞,c+i∞]X(s)exp(st)ds
- 二つの関数のたたみこみを変換すると、変換後にはただの乗算になっている。~~線形時不変システムはたたみこみで表せるので、ラプラス変換すればシステム全体を関数一つで表現できる。~~これが伝達関数で、二年冬や三年夏に扱ったもの。
線形時不変システム←[ラプラス変換]→伝達関数
線形時変システム←[??]→?
非線形システム←[??]→?
線形時不変システム以外は伝達関数では扱えない。状態空間表現や元々の微分方程式を直接扱う必要がある。
- 状態空間法
- システムに内部状態を表す変数を導入して、~~内部状態についての連立一階微分方程式と、内部状態から出力を導く方程式で表現する。
- 伝達関数での表現と比べて広い範囲のシステムを表現できる。~~システムが線形ならば状態方程式・観測方程式は線形にでき、時不変ならば方程式に陽に時間変数が現れないようにできる。
- x : 状態ベクトル~~dx/dt = f(x,t,u) :状態方程式~~y = g(x,t,u):観測方程式。出力方程式。~~状態方程式と観測方程式を合わせてシステム方程式と呼ぶ。~~講義では主に線形時不変システムを扱う。
- 線形システムの解
- dx/dt = Ax + Bu~~y = Cx + Du~~Aはtに依存してもよいとする。
- まず同次方程式を解く。~~dx/dt = Ax
- 標準基底e[i]を使って、初期値e[i]のときの解をφ[i]、それを横に並べたものをΦとすると、~~dφ[i]/dt = Aφ[i]~~dΦ/dt = AΦ~~Φ(0) = Iが成立。~~一般解はx(t) = Φ(t)x(0) で表せる。
- 元の方程式の解は、x(t) = Φ(t)x(0) + ∫[0,t]Φ(t-τ)B(τ)u(τ)dτ
- 線形時不変システムの解
- dx/dt = Ax + Bu~~y = Cx + Du~~Aはtに依存しない定行列
- (d/dt - A)x = exp(At)(d/dt)exp(-At)x(t) = Bu(t)~~x(t) = exp(At)x(0) + ∫[0,t]exp(A(t-τ))Bu(τ)dτ
- 伝達関数表現では、X(s) =(sI-A)^(-1){x(0)+BU(s)}~~(sI-A)^(-1)にあたるのがexp(At)、(たたみこみが積に変わっている)
- exp(At)?
- (d/dt)exp(At) = Aexp(At)~~Aの固有ベクトル Au = λu への作用させると、exp(At)u = exp(λt)u~~固有ベクトルの方向にexp(λt)だけ伸ばす。
- detP≠0となる行列について、~~P exp(At) P^(-1) = exp(PAP^(-i)t) :合同変換は中に素通り。
- AとBが可換ならば、exp(At)exp(Bt)=exp((A+B)t)が成立。非可換ならばそうなるとは限らない。
- 行列
 をジョルダン標準型に
をジョルダン標準型に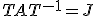 に標準化すると、
に標準化すると、
(中略)
状態空間表現での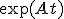 をラプラス変換すると
をラプラス変換すると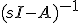
線形時不変システムの状態空間表現と伝達関数表現の対応。
- 安定性
- 平衡点
状態空間表現でのシステム 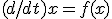 について、
について、
![f(x[e]) = 0](./cache/87549c89798b0125e8e515fd9647a0a0.mimetex.gif) となる点を平衡点と呼ぶ。
となる点を平衡点と呼ぶ。
- 平衡点まわりの安定性
任意の正数 に対して、
に対して、![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が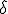 未満である初期値から時間を進めたときに、
未満である初期値から時間を進めたときに、
それより先の任意の時点で![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が 未満に留まるような正数
未満に留まるような正数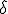 が存在するなら、その系は安定。
が存在するなら、その系は安定。
さらに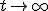 で
で![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) に収束するなら、その系は漸近安定であるという。
に収束するなら、その系は漸近安定であるという。
- 線形時不変システム
![x = \exp(At)x[0]](./cache/d5039c58bcb3e254aa1a35c1536d7eec.mimetex.gif) について、
について、
ジョルダン標準系に直して、![Tx = T\exp(At)T^{-1}Tx[0] = \exp(Jt)Tx[0]](./cache/05c778554753be3ae43630c097488470.mimetex.gif)
 の安定性と
の安定性と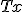 の安定性は一致する。
の安定性は一致する。
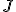 の固有値の実部が全て負ならば、
の固有値の実部が全て負ならば、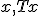 は原点に漸近安定。
は原点に漸近安定。
実部が正の固有値があれば、不安定。
固有値の実部が全て正ではなく、実部が0の固有値がサイズ2以上のジョルダンブロックを成すなら不安定。
それ以外なら安定。
- リアプノフの定理。
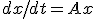 について、
について、
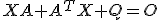 となる正定値行列
となる正定値行列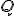 と対称行列
と対称行列 について、
について、
 が漸近安定であることと
が漸近安定であることと が正定値であることは同値。
が正定値であることは同値。
 が一意であることは講義では証明略。
が一意であることは講義では証明略。
 として
として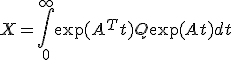 を選ぶと、正値対称。
を選ぶと、正値対称。
![[\exp(A^T t)Q\exp(At)]_0^{\infty} = \int_0^{\infty}(d/dt)\exp(A^T t)Q\exp(At)dt = A^T X+XA](./cache/fba5b8711acb7a94442ab4261ab0b023.mimetex.gif)
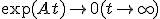 ならば、左辺は
ならば、左辺は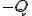 になるから、
になるから、 は
は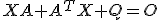 の正値対称な解になっている。
の正値対称な解になっている。
もし が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを
が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを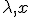 として、
として、
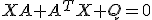 から、
から、
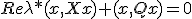 だが、各項が正なので、
だが、各項が正なので、
この式は不成立。よって には実部が非負の固有値は存在しない。
には実部が非負の固有値は存在しない。
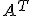 は
は の転置
の転置
- 動的システムの構造
- 相似変換
について、
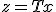 と変数変換すると、各係数は
と変数変換すると、各係数は
と変換される。
どちらも同じ入力に対して同じ出力を返す、同じシステムの別な表現になっている。
入出力関係を変えない変換を、相似変換と呼ぶ。
状態空間表現には、相似変換の分だけ任意性が残っている。
- モード分解
状態空間表現の任意性を使って、方程式を理解しやすい形に書き直す。
 をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに
をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに
独立した小さな微分方程式に分解できる。
分解された各方程式は、各固有値に対応するモードと呼ばれる。
- 可制御性(Controllability)
- 線形時不変システム
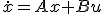 について、
について、
任意の初期値に対して、適切な入力をとれば有限時間内に、
 を原点に到達させることができるとき、
を原点に到達させることができるとき、
このシステムは可制御であるという。
- この微分方程式の解は、
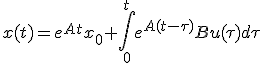
時刻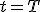 で原点に到達したとすると、
で原点に到達したとすると、
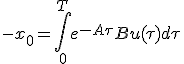 が成立する。
が成立する。
この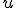 に対して、初期値
に対して、初期値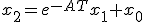 で始めることを考えれば、
で始めることを考えれば、
可制御性とは、任意の入力に対して任意の位置に持っていけるかどうかを表すとも考えられる。
- 定理
線形時不変システムが可制御であるための必要十分条件は、
可制御性行列 ![U_c = [B,AB,A^2 B,...,A^{n-1}B]](./cache/e3d426c4d1887bcdf34951b71a2f20ee.mimetex.gif) のランクがnであることである。
のランクがnであることである。
nは状態ベクトルの次元。
- 証明
- 可制御であるためには
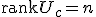 が必要。
が必要。
ケーリー・ハミルトンの定理を使えば、任意のn次正方行列の多項式は、(n-1)次以下の多項式で表せるので、
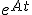 の各項を(n-1)次以下の多項式で書けば、
の各項を(n-1)次以下の多項式で書けば、
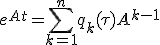 と表せる。
と表せる。
これを使って解を変形すると、
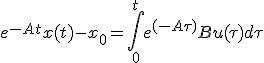
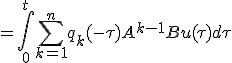
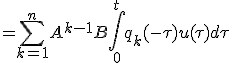
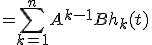
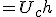
左辺は任意に動かしうる。任意の左辺に対して、等式を成り立たせる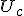 が存在するためには
が存在するためには
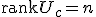 が必要。
が必要。
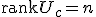 ならば可制御。
ならば可制御。
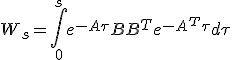
入力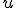 を
を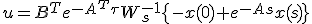
と取ってやれば、
目標の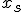 を実現する入力になっている。
を実現する入力になっている。
途中で使っている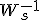 が存在すれば可制御。
が存在すれば可制御。
もし、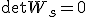 となる
となる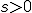 が存在するなら、
が存在するなら、
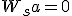 となる非零ベクトルaが存在する。
となる非零ベクトルaが存在する。
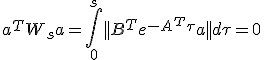
ノルムの値は非負なので、等式が成り立つためには、被積分関数は常に零である必要がある。
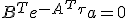
この式を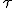 で
で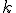 階微分して
階微分して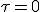 とすれば、
とすれば、
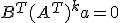
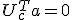
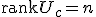 ならば、このようなaは存在しない、
ならば、このようなaは存在しない、
ゆえに、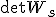 は常に非零で、このシステムは可制御。
は常に非零で、このシステムは可制御。
- 可観測性
- ある有限の時間
![[0,s]](./cache/1991ec20dd30cc37221ce3425a7c5b66.mimetex.gif) の入出力の測定から、
の入出力の測定から、
内部状態の初期値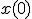 を唯一に決定できるとき、
を唯一に決定できるとき、
そのシステムは可観測(observable)という。
- 定理
線形時不変システムが可観測であるための必要十分条件は、
可観測性行列![U_o=[C,CA,CA^2,...,CA^{n-1}]^{T}](./cache/36f16e0f4e804e8491913e03da090062.mimetex.gif) (
(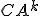 を縦に並べた行列)の
を縦に並べた行列)の
ランクがnであること。
証明はプリントで。
- 正準分解と最小実現
- 線形時不変システム,主システム
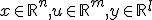
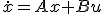
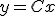 に対して、
に対して、
双対システム
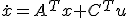
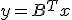 を考えると、
を考えると、
主システムの可制御性と双対システムの可観測性は同値。
主システムの可観測性と双対システムの可制御性は同値。
片方の可制御性行列は、もう片方の可観測性行列の転置。
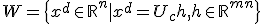 は「可制御な部分空間」
は「可制御な部分空間」
可制御系については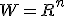
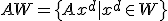 は、ケーリー・ハミルトンの定理で
は、ケーリー・ハミルトンの定理で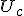 の中の
の中の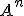 の次数下げをすれば、
の次数下げをすれば、
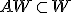 が成立。可制御な空間からの時間発展は可制御。
が成立。可制御な空間からの時間発展は可制御。
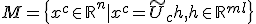 を定義すると、
を定義すると、
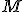 は可観測な部分空間。
は可観測な部分空間。
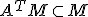 も成立。可観測な空間の時間発展は可観測
も成立。可観測な空間の時間発展は可観測
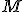 の直交補空間
の直交補空間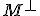 を考えると、
を考えると、
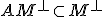
- 以上の集合を使って、以下の集合を定義すれば、
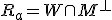 可制御で、可観測でない
可制御で、可観測でない
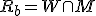 可制御で可観測
可制御で可観測
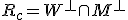 可制御でなく、可観測でもない
可制御でなく、可観測でもない
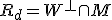 可制御でなく、可観測
可制御でなく、可観測
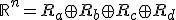 と直和分解できる。
と直和分解できる。
- それぞれの部分空間の時間発展を考えると、
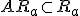
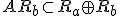
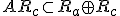
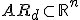 となる。
となる。
それぞれの空間の基底をとって、
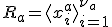
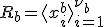
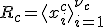
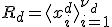
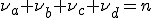
基底を初期値に時間発展を考えれば、
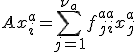
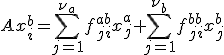
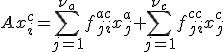
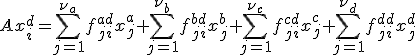
- 各部分空間の基底を使って、
![B = [x^{a}_1,x^{a}_2,...,x^{a}_{\nu_a}]G^a + [x^{b}_1,x^{b}_2,...,x^{b}_{\nu_b}]G^b](./cache/b9faf2b2c43809311beda2a45ff068cf.mimetex.gif)
各部分空間の基底を横に並べた行列を として変換をすると、
として変換をすると、
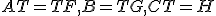
![F=\left[\begin{matrix}F^{aa} & F^{ab}& F^{ac} & F^{ad}\\0 & F^{bb} & 0 & F^{bd}\\0 & 0 & F^{cc} & F^{cd}\\0 & 0 & 0 & F^{dd}\end{matrix}\right]](./cache/9778607b93960dca0014dba1b98bc0cb.mimetex.gif)
(by yambi)
- 以上の行列を使って、
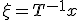 と変換すれば。
と変換すれば。
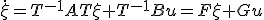
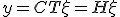 となる。これを正準分解という。
となる。これを正準分解という。
これをブロック線図で表すと、入力は可制御な空間である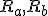 へ
へ
出力は可観測な空間である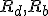 から繋がり、
から繋がり、
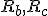 は独立。
は独立。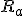 は他全てから影響を受け、
は他全てから影響を受け、
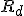 は他全てに影響を及ぼす。
は他全てに影響を及ぼす。
- 最小実現
- 正準分解した上で入力から出力への伝達関数を書いてみると、
伝達関数が表しているのは、可制御かつ可観測な部分空間の成分だけであることがわかる。
- 可制御かつ可観測な部分空間の成分を取り出しても、入出力関係は変わらない。
これをこのシステムの最小実現と呼ぶ。
- MIMOでの零点
- システムを表す行列を[[(sI-A), B],[C,D]]と並べたときに、
この行列をランク落ちさせるsをこのシステムの不変零点と呼ぶ。
この定義はSISOでの零点の定義の一般化になっている。
- 極配置問題
- SISOの可制御系
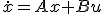 について、
について、
内部状態 を観測し、
を観測し、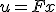 とフィードバックすることを考える。
とフィードバックすることを考える。
このようなフィードバックを『状態フィードバック』と呼ぶ。
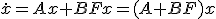
可制御標準形に変換して、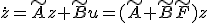
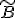 は最後の行が1で、それ以外がすべて0の縦ベクトルなので、
は最後の行が1で、それ以外がすべて0の縦ベクトルなので、
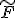 の項は第n行にしか効いてこない。
の項は第n行にしか効いてこない。
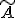 の第n行は、Aの特性多項式の係数。
の第n行は、Aの特性多項式の係数。
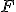 を掛けてフィードバックすることは、特性多項式の係数をずらすことになる。
を掛けてフィードバックすることは、特性多項式の係数をずらすことになる。
特定の場所に伝達関数の極を配置したいときには、その極を根に持つ多項式を作り、
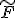 の値を調節して、特性多項式の係数をずらして、その多項式を作ってやれば良い。
の値を調節して、特性多項式の係数をずらして、その多項式を作ってやれば良い。
こうして、可制御系については閉ループ系の極は任意の位置に配置でき、常に安定化できる。
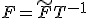
- レポート問題、12/10まで。
- コンデンサと抵抗を並列に繋げた回路と、コイルと抵抗を並列に繋げた回路を直列に繋いだ回路について、
回路全体に流れる電流を入力、出力電圧を出力、
コンデンサにかかる電圧と、コイルに流れる電流を内部状態として、
可制御性行列と伝達関数を調べ、可制御性との関係を述べよ。
- 長さ・質量の異なる振り子について、振り子の振れ幅とその速度についての可制御性と
振り子の長さ・重りの質量の関係を調べよ。振り子の振れ幅は微小としてよい。
- SISO可制御正準系の
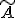 について、
について、![|sI-\tilde{A}| = s^n + \sum_{k_1}^{n}a[k]s^{k+1}](./cache/ab838a177124d9ba0afc6cfd1caad89c.mimetex.gif) を計算せよ。
を計算せよ。
![\dot{x} = [[1,2],[-3,-4]]x + [2,3]u](./cache/aca4f9a02b3d1b2ee738c25f3116c573.mimetex.gif) について、
について、
状態フィードバックにより、極を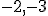 に配置したい。
に配置したい。
- 直接的にFを求めよ。
- 可制御正準系に直してからFを求めよ。
- 状態推定
- オブザーバ
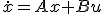
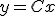 について、入出力信号を観測して、
について、入出力信号を観測して、 を推定することを考える。
を推定することを考える。
 と同じ方程式に従う別な系
と同じ方程式に従う別な系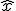 を用意すると、
を用意すると、
誤差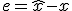 は
は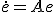 に従い、
に従い、
 が漸近安定ならば誤差は0へ漸近し、不安定ならば発散してしまう。
が漸近安定ならば誤差は0へ漸近し、不安定ならば発散してしまう。- 代わりに
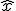 として、
として、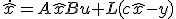 を使うことを次次次回考える。
を使うことを次次次回考える。
- 最適レギュレータ問題
アクチュエータに使うエネルギーと目標地点への制御の重み付き最適化。
- 可制御系は適当な係数を掛けた状態フィードバックで安定化できる。
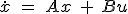
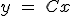
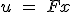 状態フィードバック
状態フィードバック
- このシステムの内部状態や出力の変化を明示すれば
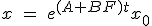
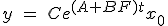
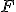 をうまく選んで、任意の初期値に対して
をうまく選んで、任意の初期値に対して
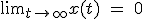 となるようにする。
となるようにする。
システムが可制御であれば、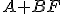 の固有値は任意に設定可能。
の固有値は任意に設定可能。
では具体的に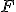 はどう決めるのがよいか。
はどう決めるのがよいか。
- 評価関数(Performance Index)
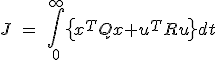 という評価関数を作って、これを最小化する。
という評価関数を作って、これを最小化する。
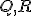 は状態,制御入力に対する重み行列。
は状態,制御入力に対する重み行列。
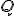 は半正値対称、
は半正値対称、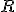 は正値対称に選ぶ。
は正値対称に選ぶ。
これは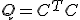 と選ぶと
と選ぶと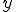 の値で評価したことになる。
の値で評価したことになる。
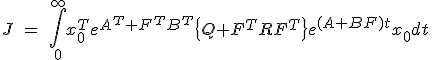 を最小とする
を最小とする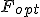 は、
は、
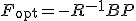 の形で与えられる。
の形で与えられる。
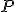 はRiccati方程式
はRiccati方程式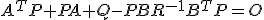 の解で、正値対称行列。
の解で、正値対称行列。
可制御で可観測なシステムについては、解は常に存在し、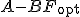 は安定になる。
は安定になる。
 の安定性を仮定すると、任意の正値対称行列
の安定性を仮定すると、任意の正値対称行列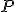 について、
について、
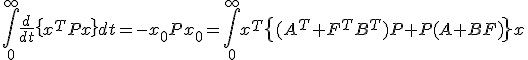 から、
から、
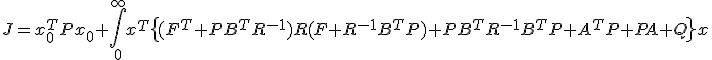 が成立。
が成立。
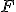 を変化させて
を変化させて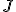 を最小化するには、
を最小化するには、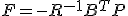 を選べばよい。
を選べばよい。
- Riccati方程式の解法
- ハミルトン行列
![H=[[A,-BR^{-1}B^{T}],[-Q,-A^T]]](./cache/83a601ba0fb11c9de94ce9e54065a93c.mimetex.gif) を定義し、固有値を求める。
を定義し、固有値を求める。
固有値は実軸・虚軸に対して対称に現れる。
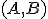 が可制御で、
が可制御で、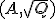 が可観測ならば虚軸上には固有値は無い。
が可観測ならば虚軸上には固有値は無い。
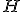 の安定な固有値・固有ベクトルn個を並べたものを
の安定な固有値・固有ベクトルn個を並べたものを![\Lambda,[U,V]^{T}](./cache/6380278add13f39dbf1dd6b18e367d07.mimetex.gif) とすると、
とすると、
![[UV^{-1},-I]H[U,V]^{T} = [UV^{-1},-I][U,V]^{T}\Lambda = 0](./cache/16761940283efc7b6736b9d715e080c3.mimetex.gif) が成立。
が成立。
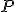 として
として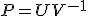 をとると、PはRiccati方程式の解になっている。
をとると、PはRiccati方程式の解になっている。
これでRiccati方程式を2n次正方行列であるハミルトン行列Hの固有値問題に帰着できた。
- Riccati方程式の解について、
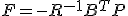
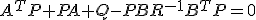
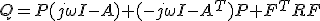 と変形し、
と変形し、
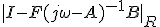 を考えると、
を考えると、
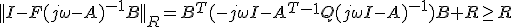 が任意の
が任意の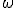 について成立。
について成立。
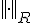 は
は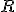 を計量とする内積。
を計量とする内積。
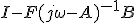 は、最適レギュレータをかけたときの一巡伝達関数。
は、最適レギュレータをかけたときの一巡伝達関数。
この不等式が意味するところは、任意の周波数の入力に対し、
外乱に対する強度を示す感度関数の値を1より小さく保てること。
- 制御入力に対する重みを無限大にして、最適制御をかけたときの閉ループ伝達関数は、
開ループ伝達関数の不安定極を虚軸対称に反転させたもの。
制御対象に対する重みを無限大にして、最適制御をかけたときの閉ループ伝達関数は、
不安定極を虚軸対称に反転させ、他の極は∞に飛ばした形になる。
- 状態推定
- オブザーバ
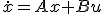
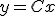 の入出力を観測してxを推定する。
の入出力を観測してxを推定する。
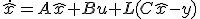 と変数を設定する。
と変数を設定する。
これを恒等オブザーバと呼ぶ。
誤差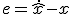 の挙動を見ると、
の挙動を見ると、
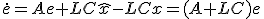
系が可制御ならば、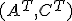 が可制御で、
が可制御で、
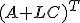 の極は任意に配置可能、
の極は任意に配置可能、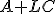 は安定化可能になる。
は安定化可能になる。
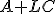 を安定化すれば
を安定化すれば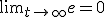
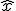 によって入出力だけから
によって入出力だけから を観測できる。
を観測できる。
- 最小次元オブザーバ
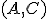 が可観測で、
が可観測で、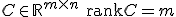 だとする。
だとする。
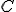 に行を追加して、正則な行列
に行を追加して、正則な行列 を作り、
を作り、
![T=\left[\begin{matrix} C \\ U \end{matrix}\right]](./cache/422097e7dca9d10422382566c5f58b26.mimetex.gif)
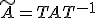 とする。
とする。![C=[I\ 0]T](./cache/410afee445b077d3a95e77e954b945de.mimetex.gif) が成立。
が成立。
![\tilde{C}=CT^{-1}=[I\ 0]](./cache/06949f01b6d7e94ca01d8b600d9048d6.mimetex.gif) とすると、
とすると、
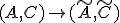 は
は による相似変換。
による相似変換。
![\tilde{A} = \left[\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22} \end{matrix}\right]](./cache/9065d406952f0e16e04738efe5b7a364.mimetex.gif) とすると、元の系が可観測であることから
とすると、元の系が可観測であることから
![\mathrm{rank}\left[\begin{matrix}A_{12}\\A_{12}A_{22}\\ \vdots \\ A_{12}A_{22}^{n-1}\end{matrix}\right] = n-m](./cache/5f7948790a0f5c48a40964f4811b2044.mimetex.gif) 、
、
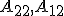 が可観測であることが得られる。
が可観測であることが得られる。
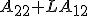 を安定化するLが存在する。
を安定化するLが存在する。
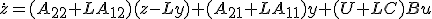 とすると、
とすると、
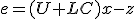 は、
は、
![\dot{e} = \left[\begin{matrix}L&I\end{matrix}\right]\left[\begin{matrix}C\\U\end{matrix}\right](Ax+Bu)-\dot{z}=(A_{22}+LA_{12})e](./cache/86eeda9c9be52e69fa4f807715de7bfa.mimetex.gif) に従う。
に従う。
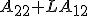 を安定化すれば、誤差
を安定化すれば、誤差 は0に収束する。
は0に収束する。
![\left[\begin{matrix}y\\z\end{matrix}\right]\to \left[\begin{matrix}I&0\\L&I\end{matrix}\right]\left[\begin{matrix}C\\U\end{matrix}\right]x](./cache/6a7f9c4de185b08d246807b93ba1c248.mimetex.gif)
![\left[\begin{matrix}C\\U\end{matrix}\right]^{-1}\left[\begin{matrix}I&0\\-L&I\end{matrix}\right]\left[\begin{matrix}y\\z\end{matrix}\right]\to x](./cache/f5741adc415d7bd9bac57070c8213c5c.mimetex.gif)
- カルマンフィルタ
フィルタ:推定対象に混入する外乱を除去するもの。
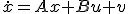
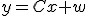 という系を考える。
という系を考える。
 はシステム雑音、
はシステム雑音、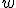 を観測雑音と呼ぶ。
を観測雑音と呼ぶ。
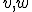 は白色雑音だと仮定する。
は白色雑音だと仮定する。
![E[v]=E[w]=0](./cache/7fe3615bf15c33ba11ca7659df96b052.mimetex.gif)
![E[v(t)v^{T}(t+\tau)] = Q\delta(\tau)](./cache/c1ea324e2ab7a5f6d65915bb2b5814ab.mimetex.gif)
![E[w(t)w^{T}(t+\tau)] = R\delta(\tau)](./cache/38dedec706679e09088bea0768da85e4.mimetex.gif)
![E[v(t)w^{T}(\tau)] = 0](./cache/d62952bd18736904054419aa53bb780b.mimetex.gif)
入出力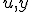 から状態
から状態 を推定する。
を推定する。
![\tilde{x}(t) = E[x(t) | y(\tau),u(\tau),\tau \leq t]](./cache/ddb74b8f17f2183c374580c06f5a24f3.mimetex.gif)
- 条件付き期待値
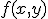 を
を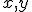 の同時確率密度だとして、
の同時確率密度だとして、
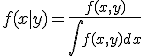 と、条件付き確率密度を定義して、
と、条件付き確率密度を定義して、
条件付き期待値を![E[x|y]=\int xf(x|y)dx](./cache/f5b2fef31180174411d699aceaf8d8f1.mimetex.gif) と定義する。
と定義する。
何らかの方法で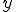 から
から の推定値
の推定値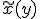 を計算できたとしたとき、
を計算できたとしたとき、
その二乗誤差の期待値には下限が存在し、![E[(x-\tilde{x})^2]\geq E[(x-E[x|y])^2]](./cache/65405195f353805665f27aba1aaf9706.mimetex.gif) となる。
となる。
- 補題:任意の関数
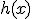 について、
について、![E[(x-E[x|y])h(y)] = 0](./cache/4316292c4899be450451f3d5e50e4661.mimetex.gif)
- 条件付き期待値
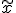 は、
は、
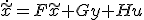 という形の微分方程式に従う。
という形の微分方程式に従う。
係数行列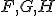 が満たすべき性質は、
が満たすべき性質は、
![E[\tilde{x}] = E[x]](./cache/2fb682a73a390ee5cd534294feebaa19.mimetex.gif)
![E[\dot{x}] = AE[x]+Bu](./cache/61913157fba6286694c58d5a7e5a7021.mimetex.gif)
![E[y] = CE[x]](./cache/55fb19dd6434976c9206c18f41a0ac26.mimetex.gif)
![E[\dot{\tilde{x}}] = E[\dot{x}] = (F+GC)E[x]+Hu](./cache/f59cff3b0ead8469d0afa07c35b89a0b.mimetex.gif) から
から
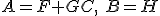
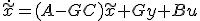
残ったGを決めるために、誤差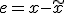 を考える。
を考える。
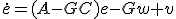
誤差の共分散行列を![\tilde{P} = E[e(t)e^{T}(t)]](./cache/4740cb01bd8e4e733ad04ad9118561e2.mimetex.gif) とすると、
とすると、
十分時間が経った後では、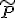 は
は
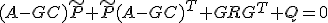 の解になっている。
の解になっている。
変形すると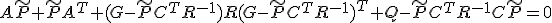
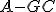 が安定ならば、
が安定ならば、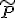 には下限
には下限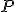 が存在し、
が存在し、
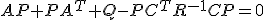 に対して
に対して
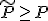 が成立。
が成立。
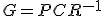 と選んでやると
と選んでやると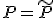 となり、
となり、
誤差の分散を最小にする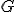 が得られた。
が得られた。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
 をジョルダン標準型に
をジョルダン標準型に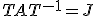 に標準化すると、
に標準化すると、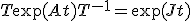
![L[\exp(Jt)] = (sI-J)^{-1}](./cache/8c913b3e4503d231d04beae52279444a.mimetex.gif)
![L[\exp(At)] = L[T^{-1}\exp(Jt)T] = T^{-1}(sI-J)^{-1} T = (sI-A)^{-1}](./cache/c0a7dd1877c3f3d84b17589175e432f1.mimetex.gif)
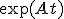 をラプラス変換すると
をラプラス変換すると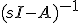
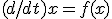 について、
について、![f(x[e]) = 0](./cache/87549c89798b0125e8e515fd9647a0a0.mimetex.gif) となる点を平衡点と呼ぶ。
となる点を平衡点と呼ぶ。 に対して、
に対して、![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が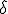 未満である初期値から時間を進めたときに、
未満である初期値から時間を進めたときに、![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が 未満に留まるような正数
未満に留まるような正数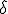 が存在するなら、その系は安定。
が存在するなら、その系は安定。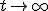 で
で![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) に収束するなら、その系は漸近安定であるという。
に収束するなら、その系は漸近安定であるという。![x = \exp(At)x[0]](./cache/d5039c58bcb3e254aa1a35c1536d7eec.mimetex.gif) について、
について、![Tx = T\exp(At)T^{-1}Tx[0] = \exp(Jt)Tx[0]](./cache/05c778554753be3ae43630c097488470.mimetex.gif)
 の安定性と
の安定性と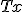 の安定性は一致する。
の安定性は一致する。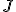 の固有値の実部が全て負ならば、
の固有値の実部が全て負ならば、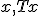 は原点に漸近安定。
は原点に漸近安定。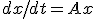 について、
について、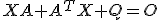 となる正定値行列
となる正定値行列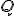 と対称行列
と対称行列 について、
について、 が漸近安定であることと
が漸近安定であることと が正定値であることは同値。
が正定値であることは同値。 が一意であることは講義では証明略。
が一意であることは講義では証明略。 として
として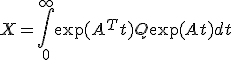 を選ぶと、正値対称。
を選ぶと、正値対称。![[\exp(A^T t)Q\exp(At)]_0^{\infty} = \int_0^{\infty}(d/dt)\exp(A^T t)Q\exp(At)dt = A^T X+XA](./cache/fba5b8711acb7a94442ab4261ab0b023.mimetex.gif)
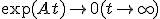 ならば、左辺は
ならば、左辺は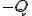 になるから、
になるから、 は
は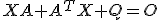 の正値対称な解になっている。
の正値対称な解になっている。 が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを
が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを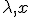 として、
として、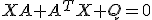 から、
から、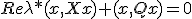 だが、各項が正なので、
だが、各項が正なので、 には実部が非負の固有値は存在しない。
には実部が非負の固有値は存在しない。
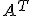 は
は の転置
の転置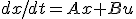
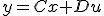
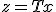 と変数変換すると、各係数は
と変数変換すると、各係数は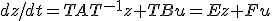
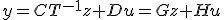
 をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに
をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに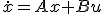 について、
について、 を原点に到達させることができるとき、
を原点に到達させることができるとき、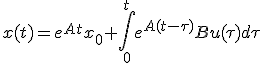
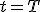 で原点に到達したとすると、
で原点に到達したとすると、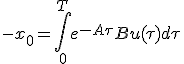 が成立する。
が成立する。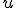 に対して、初期値
に対して、初期値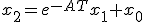 で始めることを考えれば、
で始めることを考えれば、![U_c = [B,AB,A^2 B,...,A^{n-1}B]](./cache/e3d426c4d1887bcdf34951b71a2f20ee.mimetex.gif) のランクがnであることである。
のランクがnであることである。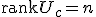 が必要。
が必要。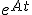 の各項を(n-1)次以下の多項式で書けば、
の各項を(n-1)次以下の多項式で書けば、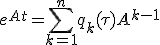 と表せる。
と表せる。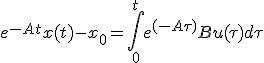
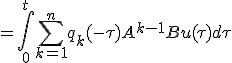
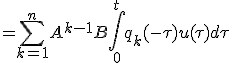
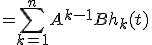
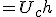
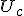 が存在するためには
が存在するためには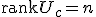 が必要。
が必要。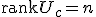 ならば可制御。
ならば可制御。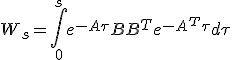
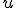 を
を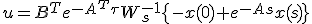
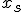 を実現する入力になっている。
を実現する入力になっている。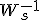 が存在すれば可制御。
が存在すれば可制御。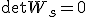 となる
となる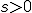 が存在するなら、
が存在するなら、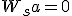 となる非零ベクトルaが存在する。
となる非零ベクトルaが存在する。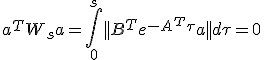
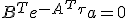
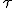 で
で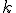 階微分して
階微分して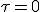 とすれば、
とすれば、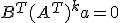
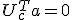
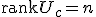 ならば、このようなaは存在しない、
ならば、このようなaは存在しない、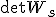 は常に非零で、このシステムは可制御。
は常に非零で、このシステムは可制御。![[0,s]](./cache/1991ec20dd30cc37221ce3425a7c5b66.mimetex.gif) の入出力の測定から、
の入出力の測定から、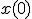 を唯一に決定できるとき、
を唯一に決定できるとき、![U_o=[C,CA,CA^2,...,CA^{n-1}]^{T}](./cache/36f16e0f4e804e8491913e03da090062.mimetex.gif) (
(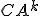 を縦に並べた行列)の
を縦に並べた行列)の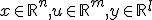
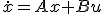
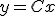 に対して、
に対して、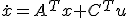
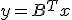 を考えると、
を考えると、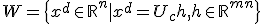 は「可制御な部分空間」
は「可制御な部分空間」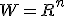
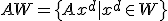 は、ケーリー・ハミルトンの定理で
は、ケーリー・ハミルトンの定理で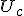 の中の
の中の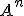 の次数下げをすれば、
の次数下げをすれば、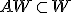 が成立。可制御な空間からの時間発展は可制御。
が成立。可制御な空間からの時間発展は可制御。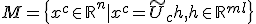 を定義すると、
を定義すると、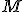 は可観測な部分空間。
は可観測な部分空間。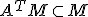 も成立。可観測な空間の時間発展は可観測
も成立。可観測な空間の時間発展は可観測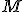 の直交補空間
の直交補空間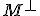 を考えると、
を考えると、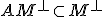
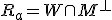 可制御で、可観測でない
可制御で、可観測でない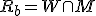 可制御で可観測
可制御で可観測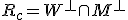 可制御でなく、可観測でもない
可制御でなく、可観測でもない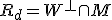 可制御でなく、可観測
可制御でなく、可観測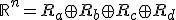 と直和分解できる。
と直和分解できる。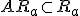
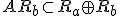
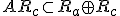
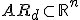 となる。
となる。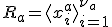
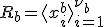
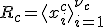
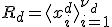
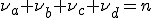
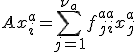
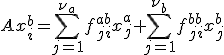
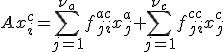
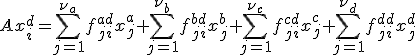
![B = [x^{a}_1,x^{a}_2,...,x^{a}_{\nu_a}]G^a + [x^{b}_1,x^{b}_2,...,x^{b}_{\nu_b}]G^b](./cache/b9faf2b2c43809311beda2a45ff068cf.mimetex.gif)
 として変換をすると、
として変換をすると、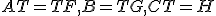
![F=\left[\begin{matrix}F^{aa} & F^{ab}& F^{ac} & F^{ad}\\0 & F^{bb} & 0 & F^{bd}\\0 & 0 & F^{cc} & F^{cd}\\0 & 0 & 0 & F^{dd}\end{matrix}\right]](./cache/9778607b93960dca0014dba1b98bc0cb.mimetex.gif)
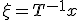 と変換すれば。
と変換すれば。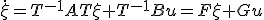
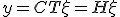 となる。これを正準分解という。
となる。これを正準分解という。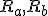 へ
へ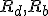 から繋がり、
から繋がり、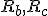 は独立。
は独立。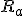 は他全てから影響を受け、
は他全てから影響を受け、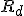 は他全てに影響を及ぼす。
は他全てに影響を及ぼす。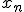 についての高階の微分方程式に帰着。
についての高階の微分方程式に帰着。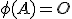
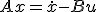
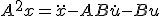
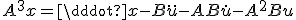
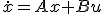 について、
について、 を観測し、
を観測し、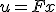 とフィードバックすることを考える。
とフィードバックすることを考える。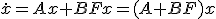
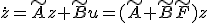
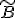 は最後の行が1で、それ以外がすべて0の縦ベクトルなので、
は最後の行が1で、それ以外がすべて0の縦ベクトルなので、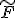 の項は第n行にしか効いてこない。
の項は第n行にしか効いてこない。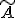 の第n行は、Aの特性多項式の係数。
の第n行は、Aの特性多項式の係数。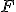 を掛けてフィードバックすることは、特性多項式の係数をずらすことになる。
を掛けてフィードバックすることは、特性多項式の係数をずらすことになる。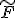 の値を調節して、特性多項式の係数をずらして、その多項式を作ってやれば良い。
の値を調節して、特性多項式の係数をずらして、その多項式を作ってやれば良い。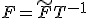
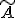 について、
について、![|sI-\tilde{A}| = s^n + \sum_{k_1}^{n}a[k]s^{k+1}](./cache/ab838a177124d9ba0afc6cfd1caad89c.mimetex.gif) を計算せよ。
を計算せよ。![\dot{x} = [[1,2],[-3,-4]]x + [2,3]u](./cache/aca4f9a02b3d1b2ee738c25f3116c573.mimetex.gif) について、
について、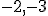 に配置したい。
に配置したい。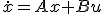
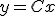 について、入出力信号を観測して、
について、入出力信号を観測して、 を推定することを考える。
を推定することを考える。
 と同じ方程式に従う別な系
と同じ方程式に従う別な系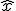 を用意すると、
を用意すると、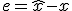 は
は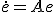 に従い、
に従い、 が漸近安定ならば誤差は0へ漸近し、不安定ならば発散してしまう。
が漸近安定ならば誤差は0へ漸近し、不安定ならば発散してしまう。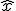 として、
として、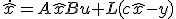 を使うことを次次次回考える。
を使うことを次次次回考える。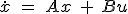
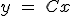
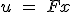 状態フィードバック
状態フィードバック
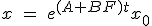
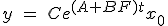
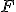 をうまく選んで、任意の初期値に対して
をうまく選んで、任意の初期値に対して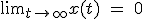 となるようにする。
となるようにする。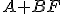 の固有値は任意に設定可能。
の固有値は任意に設定可能。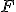 はどう決めるのがよいか。
はどう決めるのがよいか。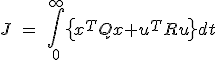 という評価関数を作って、これを最小化する。
という評価関数を作って、これを最小化する。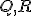 は状態,制御入力に対する重み行列。
は状態,制御入力に対する重み行列。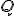 は半正値対称、
は半正値対称、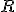 は正値対称に選ぶ。
は正値対称に選ぶ。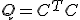 と選ぶと
と選ぶと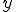 の値で評価したことになる。
の値で評価したことになる。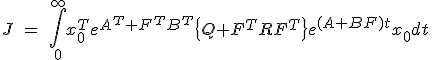 を最小とする
を最小とする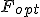 は、
は、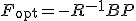 の形で与えられる。
の形で与えられる。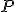 はRiccati方程式
はRiccati方程式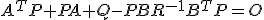 の解で、正値対称行列。
の解で、正値対称行列。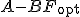 は安定になる。
は安定になる。 の安定性を仮定すると、任意の正値対称行列
の安定性を仮定すると、任意の正値対称行列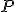 について、
について、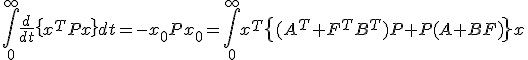 から、
から、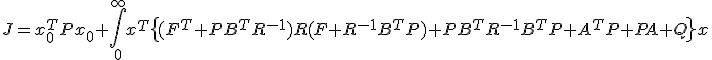 が成立。
が成立。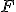 を変化させて
を変化させて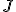 を最小化するには、
を最小化するには、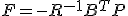 を選べばよい。
を選べばよい。![H=[[A,-BR^{-1}B^{T}],[-Q,-A^T]]](./cache/83a601ba0fb11c9de94ce9e54065a93c.mimetex.gif) を定義し、固有値を求める。
を定義し、固有値を求める。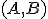 が可制御で、
が可制御で、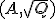 が可観測ならば虚軸上には固有値は無い。
が可観測ならば虚軸上には固有値は無い。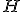 の安定な固有値・固有ベクトルn個を並べたものを
の安定な固有値・固有ベクトルn個を並べたものを![\Lambda,[U,V]^{T}](./cache/6380278add13f39dbf1dd6b18e367d07.mimetex.gif) とすると、
とすると、![[UV^{-1},-I]H[U,V]^{T} = [UV^{-1},-I][U,V]^{T}\Lambda = 0](./cache/16761940283efc7b6736b9d715e080c3.mimetex.gif) が成立。
が成立。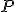 として
として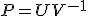 をとると、PはRiccati方程式の解になっている。
をとると、PはRiccati方程式の解になっている。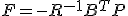
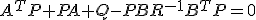
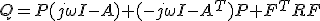 と変形し、
と変形し、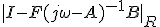 を考えると、
を考えると、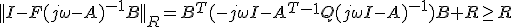 が任意の
が任意の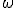 について成立。
について成立。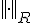 は
は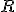 を計量とする内積。
を計量とする内積。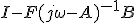 は、最適レギュレータをかけたときの一巡伝達関数。
は、最適レギュレータをかけたときの一巡伝達関数。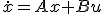
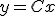 の入出力を観測してxを推定する。
の入出力を観測してxを推定する。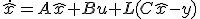 と変数を設定する。
と変数を設定する。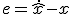 の挙動を見ると、
の挙動を見ると、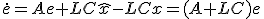
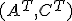 が可制御で、
が可制御で、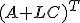 の極は任意に配置可能、
の極は任意に配置可能、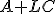 は安定化可能になる。
は安定化可能になる。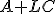 を安定化すれば
を安定化すれば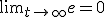
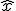 によって入出力だけから
によって入出力だけから を観測できる。
を観測できる。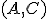 が可観測で、
が可観測で、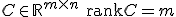 だとする。
だとする。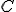 に行を追加して、正則な行列
に行を追加して、正則な行列 を作り、
を作り、![T=\left[\begin{matrix} C \\ U \end{matrix}\right]](./cache/422097e7dca9d10422382566c5f58b26.mimetex.gif)
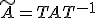 とする。
とする。![C=[I\ 0]T](./cache/410afee445b077d3a95e77e954b945de.mimetex.gif) が成立。
が成立。
![\tilde{C}=CT^{-1}=[I\ 0]](./cache/06949f01b6d7e94ca01d8b600d9048d6.mimetex.gif) とすると、
とすると、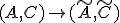 は
は による相似変換。
による相似変換。![\tilde{A} = \left[\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22} \end{matrix}\right]](./cache/9065d406952f0e16e04738efe5b7a364.mimetex.gif) とすると、元の系が可観測であることから
とすると、元の系が可観測であることから![\mathrm{rank}\left[\begin{matrix}A_{12}\\A_{12}A_{22}\\ \vdots \\ A_{12}A_{22}^{n-1}\end{matrix}\right] = n-m](./cache/5f7948790a0f5c48a40964f4811b2044.mimetex.gif) 、
、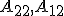 が可観測であることが得られる。
が可観測であることが得られる。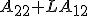 を安定化するLが存在する。
を安定化するLが存在する。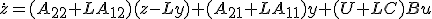 とすると、
とすると、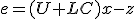 は、
は、![\dot{e} = \left[\begin{matrix}L&I\end{matrix}\right]\left[\begin{matrix}C\\U\end{matrix}\right](Ax+Bu)-\dot{z}=(A_{22}+LA_{12})e](./cache/86eeda9c9be52e69fa4f807715de7bfa.mimetex.gif) に従う。
に従う。
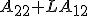 を安定化すれば、誤差
を安定化すれば、誤差 は0に収束する。
は0に収束する。![\left[\begin{matrix}y\\z\end{matrix}\right]\to \left[\begin{matrix}I&0\\L&I\end{matrix}\right]\left[\begin{matrix}C\\U\end{matrix}\right]x](./cache/6a7f9c4de185b08d246807b93ba1c248.mimetex.gif)
![\left[\begin{matrix}C\\U\end{matrix}\right]^{-1}\left[\begin{matrix}I&0\\-L&I\end{matrix}\right]\left[\begin{matrix}y\\z\end{matrix}\right]\to x](./cache/f5741adc415d7bd9bac57070c8213c5c.mimetex.gif)
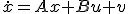
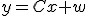 という系を考える。
という系を考える。 はシステム雑音、
はシステム雑音、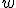 を観測雑音と呼ぶ。
を観測雑音と呼ぶ。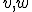 は白色雑音だと仮定する。
は白色雑音だと仮定する。![E[v]=E[w]=0](./cache/7fe3615bf15c33ba11ca7659df96b052.mimetex.gif)
![E[v(t)v^{T}(t+\tau)] = Q\delta(\tau)](./cache/c1ea324e2ab7a5f6d65915bb2b5814ab.mimetex.gif)
![E[w(t)w^{T}(t+\tau)] = R\delta(\tau)](./cache/38dedec706679e09088bea0768da85e4.mimetex.gif)
![E[v(t)w^{T}(\tau)] = 0](./cache/d62952bd18736904054419aa53bb780b.mimetex.gif)
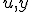 から状態
から状態 を推定する。
を推定する。![\tilde{x}(t) = E[x(t) | y(\tau),u(\tau),\tau \leq t]](./cache/ddb74b8f17f2183c374580c06f5a24f3.mimetex.gif)
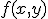 を
を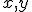 の同時確率密度だとして、
の同時確率密度だとして、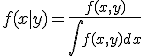 と、条件付き確率密度を定義して、
と、条件付き確率密度を定義して、![E[x|y]=\int xf(x|y)dx](./cache/f5b2fef31180174411d699aceaf8d8f1.mimetex.gif) と定義する。
と定義する。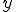 から
から の推定値
の推定値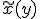 を計算できたとしたとき、
を計算できたとしたとき、![E[(x-\tilde{x})^2]\geq E[(x-E[x|y])^2]](./cache/65405195f353805665f27aba1aaf9706.mimetex.gif) となる。
となる。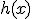 について、
について、![E[(x-E[x|y])h(y)] = 0](./cache/4316292c4899be450451f3d5e50e4661.mimetex.gif)
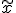 は、
は、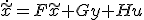 という形の微分方程式に従う。
という形の微分方程式に従う。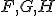 が満たすべき性質は、
が満たすべき性質は、![E[\tilde{x}] = E[x]](./cache/2fb682a73a390ee5cd534294feebaa19.mimetex.gif)
![E[\dot{x}] = AE[x]+Bu](./cache/61913157fba6286694c58d5a7e5a7021.mimetex.gif)
![E[y] = CE[x]](./cache/55fb19dd6434976c9206c18f41a0ac26.mimetex.gif)
![E[\dot{\tilde{x}}] = E[\dot{x}] = (F+GC)E[x]+Hu](./cache/f59cff3b0ead8469d0afa07c35b89a0b.mimetex.gif) から
から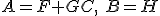
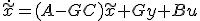
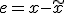 を考える。
を考える。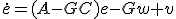
![\tilde{P} = E[e(t)e^{T}(t)]](./cache/4740cb01bd8e4e733ad04ad9118561e2.mimetex.gif) とすると、
とすると、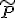 は
は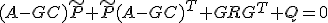 の解になっている。
の解になっている。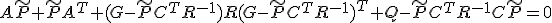
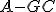 が安定ならば、
が安定ならば、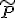 には下限
には下限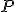 が存在し、
が存在し、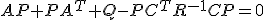 に対して
に対して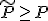 が成立。
が成立。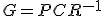 と選んでやると
と選んでやると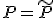 となり、
となり、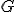 が得られた。
が得られた。