制御論第二のバックアップ(No.2)

プログラムの数理
- 月2
- 1.5単位数理C システムB
- 10:15～11:45 ＠63

教科書
- システム制御理論入門実教出版

序論
- 古典制御理論から現代制御理論へ
  - 古典制御理論:(19世紀後半～1930年代)
    マクスウェルによるガバナーの解析。蒸気機関の制御。
    ラウス・フルビッツの安定判別法。
    伝達関数によるシステムの表現。
    周波数領域。ナイキストの安定判別。
    時間領域。PID制御。
    ウィナーフィルタ。
  - 古典制御の利点~実験的に得やすい入出力特性に基づいて解析・設計する。
    計算量は少ない。
    直感的
  - 古典制御の欠点
    複雑なシステムの設計には向かない。
    システムの内部状態を無視している。
    方法論としての工学。理論よりも実践が優先。
  - シャノンの情報理論(1948年)
    「通信」の一般化
    情報量と通信容量の関係。
    情報量についての普遍的法則を発見。
    モデルや表現法に依存しない一般法則。
  - カルマンの最終目標
    制御に関する純粋理論
    望ましい制御を実現するためにはどのような、そしてどれくらいの情報が必要であるか？
    与えられたプラントを、制御という観点から完全に特徴付ける本質的な特徴は何か？
  - カルマン(1959年～1960年代)
    制御問題の本質を明らかにすること。
    内部状態変数。
    可制御性・可観測性。
    状態推定とフィードバック制御

動的システムと状態方程式
- 動的システム
  - 粘性抵抗とダンパのシステム。
    
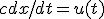
    $c dx/dt = u(t)$
```
dx/dt = u(t)/c = f(u(t))
```
    ある時点でのシステムの状態は、初期状態と入力の履歴で定まる。
```
x = (1/c)∫[0,t]u(τ)dτ + x(0)
```
    力 u(t) を入力、位置 x(t) を出力とするシステムと見なせる。
  - 動的システム(Dynamical System)
    入力と出力のあるシステムで、初期状態と入力の履歴により、任意の時刻の状態が定まるもの。
  - 静的システム(Static System)
    入力と出力のあるシステムで、その時刻での入力だけからその時刻の出力が定まるもの。
    内部状態のないシステム。
  - 因果性(Causality)
    ある時刻の出力が、それより過去の入力のと初期状態のみによって定まること。
    出力が未来の入力に依存しないこと。
    ある時点から先の入力をカットしても、それ以前の出力はカットしないときと同じになること。
    物理的なシステムは全て因果的。音声フィルタなど、因果的でないシステムも作り得る。

状態方程式
- マス・バネ・ダンパー系。
  運動方程式：{M(d/dt)^2 + c(d/dt) + k}x(t) = u(t)
  出力方程式：y(t) = x(t)
  内部状態の次元を増やして、運動方程式を一階微分にする。
```
''x'' = (x[1],x[2]) = (x,dx/dt)
(d/dt)x[1] = x[2]
(d/dt)x[2] = (u-cx[2]-kx[1])/M
y = x[1]
```
  と変形すると。
```
''x'' = f(''x'',u)
y=g(''x'',u)
```
  の形で表せる。
- システムの状態方程式表示
  入力：u(t)
  出力：y(t)
  状態変数：x(t)を使って、
  状態方程式：dx/dt = f(x,u,t)
  出力方程式：y = g(x,u,t)の形でシステムを記述する。
  入力・出力・状態変数は多次元になりうる。
  入出力が共に一次元のシステムを、一入出力システム(SISO System)
  入出力が多次元のシステムを、多入出力システム(MIMO System)と呼ぶ。

線形時不変システム
- 十分長い時間、入出力が共に0となっているとする。
  動的システムP：y(t)=P[u(t)]について、
  任意の入出力関係 y_1 = P[u_1], y_2 = P[u_2] の間に、
  線形性：αy_1 + βy_2 = P[αu_1+βu_2]が成り立つとき、
  Pは線形であるという。
  状態方程式・出力方程式が線形。
- システムが任意の時間シフトについて
```
y(t+τ) = P[u(t+τ)]
```
  となるとき、Pは時不変であるという。
  状態方程式・出力方程式に陽にtを含まない。
- 例）
```
dx/dt = ax + u, y = x
y = ∫[0,t]exp(a(t-τ))u(τ)dτ
```
  は線形時不変システム。

伝達関数
状態空間法
安定性

動的システムの構造
- 相似変換
- モード分解
- 可制御性
- 可観測性
- 正準分解と最小実現
- 正準形
- 極配置問題
状態推定
- オブザーバー
- 最小次元オブザーバー
- カルマンフィルター
フィードバック制御
- レギュレータ問題
- サーボ問題
- 最適制御
- 非線形システムの線形化

制御論第二 のバックアップ(No.2)

制御論第二のバックアップ(No.2)