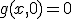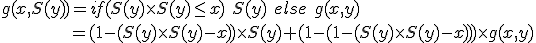情報論理 †
- 担当:萩谷昌巳教授
- 2.0単位
- 10:15-11:45 化東236
- 評価:出席,中間試験,期末試験
http://nicosia.is.s.u-tokyo.ac.jp/~hagiya/#lecture
内容 †
- 2項関係 R
- 反射的:
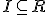 ,最小の反射的閉包:
,最小の反射的閉包: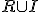
- 推移的:
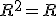 ,最小の推移的閉包:
,最小の推移的閉包: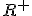
- 対称的:
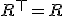 ,最小の対称的閉包:
,最小の対称的閉包: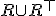
- 反対称的:
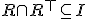
- 命題論理:
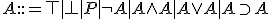
- 一階述語論理:
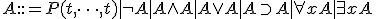
- コンパクト性:論理式の集合に対して,その任意の有限部分集合が個別に充足可能ならば,集合全体を同時に充足可能
- 完全性
- 弱い完全性:
 が充足不能
が充足不能
- 強い完全性:

- 健全性:

- 帰納的関数
- 原始帰納的関数
- zero():定数0
- 後者関数S
- 射影関数pr
- 合成:
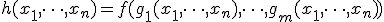
- 原始帰納法:
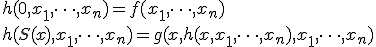
- 部分帰納的関数
- KleeneのT述語
- T(e, x, y) = 0 (if y はチューリング機械 e が入力 x で実行されたときの実行過程)
- T(e, x, y) = 1 (otherwise)
- チューリングマシンの停止性判定
- h(p(e,x))=0 (if
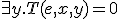 )
)
- h(p(e,x))=1 (otherwise)
- hは計算不能
- hが計算可能であると仮定すると,h(p(x,x))=0ならば停止せず,h(p(x,x))=1ならば停止するようなチューリングマシンMを構成することができるが,MにMのインデックスを入力すると矛盾する.
- 帰納的集合
- 機能的に加算
- 帰納的
- Rと
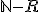 の両方が帰納的に加算
の両方が帰納的に加算
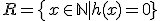
- ゲーデルの不完全性定理
- ω無矛盾
![\exists x A[x]](./cache/844a9eaf5ccabc104a86254926085c0c.mimetex.gif) が証明でき,
が証明でき,![\forall y.\neg A[\bar{y}]](./cache/08c34a3f38b0c757a95f27890ef53432.mimetex.gif) が証明できるような論理式A[y]が存在しない.
が証明できるような論理式A[y]が存在しない.
- ω矛盾かあちゃん
- 母親「あれはしちゃだめ、これもしちゃだめ…」
子供「ねぇ、何かしていい事はあるの?」
母親「ええ、あるわよ。でもあれもだめ、これもだめ…」
- ゲーデルの不完全性定理
- 算術の演繹体系がω無矛盾であると仮定すると,
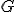 も
も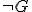 を証明することはできない.
を証明することはできない.
過去問 †
- 1.
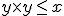 を満たす最大のyを返すような関数f(x)=g(x,x)を原始帰納法を用いてあらわせ.
を満たす最大のyを返すような関数f(x)=g(x,x)を原始帰納法を用いてあらわせ.
- 解
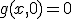
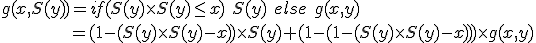
- 2.停止判定のチューリングマシンが存在するならば矛盾する
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
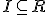 ,最小の反射的閉包:
,最小の反射的閉包: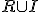
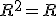 ,最小の推移的閉包:
,最小の推移的閉包: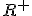
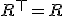 ,最小の対称的閉包:
,最小の対称的閉包: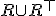
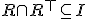
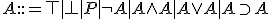
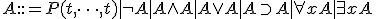
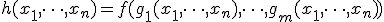
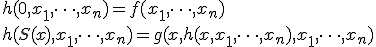
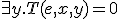 )
)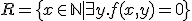
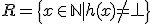
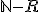 の両方が帰納的に加算
の両方が帰納的に加算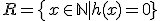
![\exists x A[x]](./cache/844a9eaf5ccabc104a86254926085c0c.mimetex.gif) が証明でき,
が証明でき,![\forall y.\neg A[\bar{y}]](./cache/08c34a3f38b0c757a95f27890ef53432.mimetex.gif) が証明できるような論理式A[y]が存在しない.
が証明できるような論理式A[y]が存在しない.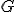 も
も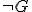 を証明することはできない.
を証明することはできない.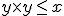 を満たす最大のyを返すような関数f(x)=g(x,x)を原始帰納法を用いてあらわせ.
を満たす最大のyを返すような関数f(x)=g(x,x)を原始帰納法を用いてあらわせ.