カイ二乗適合度検定の例のバックアップ(No.3)

バックアップ一覧
差分を表示
現在との差分を表示
ソースを表示
カイ二乗適合度検定の例へ行く。
- 1 (2008-01-08 (火) 20:36:47)
- 2 (2008-01-09 (水) 14:30:05)
- 3 (2008-01-10 (木) 11:25:36)

応用統計学

概要 †

帰無仮説をたてる＞日本人の母集団比率がA:O:B:AB=4:3:2:1である。
教室では A:13人, O:12人, B:12人, AB:4人であった。
よってχ2乗値は2.47651となる。
帰無仮説の下で多数の試行を行い、χ2乗の値を比べる。
χ2乗の値は、確率が低くなれば大きくなるという特性を持つ(誤差の2乗の値が大きくなる)。
χ2乗の値が2.47651より大きい確率を調べる。
- 確率が大きいならば2.47651というχ2乗値は、期待値に近い値だったということ。
- 確率が小さいならば2.47651というχ2乗値は、期待値から遠い(確率的にあまり起こりえない)値だったということ。
  - なぜならば、χ2乗の値がより大きい値をとる例は、より起こりにくい。より起こりにくいことは、あまり起こらない、つまり確率が小さくなる。より起こりにくいことが起こることが多いということは(上)、その値はおこりやすいと考えてよい。
大体40～50%となるはず。この確率について考察する。
通常この仮説が正しいか考える水準を(有意水準)1%や5%としてとるそれよりもはるかに大きい値なので、仮説にそう結果だと考えていい。

↑

実際 †

プログラムを書く

下のはtakoの例、コンパイルにはdSFMTのライブラリが必要。探すか解読してね。

そのまんまコピーはやめといたほうがいいよ

	#include <stdio.h>
	#include <math.h>
	#include <stdlib.h>
	#include <time.h>
	
	
	#define COUNT 41
	#define TIMES 10000
	
	#define SFMT_MEXP 19937
	#define HAVE_SSE2 1
	
	#include "dSFMT.c"
	
	double calc_kai2(double kimu[4],int dat[4]);
	void gennum(int cnt,double kimu_prob[4],int gen[4]);
	
	//A O B AB
	int main(void){
		//帰無仮説の確率
		double kimu_prob[4]={0.4,0.3,0.2,0.1};
		double kimu[4];
		//genは演算用、realに実際の教室での人数が入る
		int gen[4],real[4]={13,12,12,4};
		//TIMES(試行)回数分χ2乗値を格納する
		double kai2s[TIMES],kai2,prob_big;
		int i,bigger_cnt;
		
		int seed=(unsigned) time(NULL);
		init_gen_rand(seed);
		
		for(i=0;i<4;i++){
			kimu[i]=COUNT*kimu_prob[i];
		}
		printf("kr0:%f\n",kimu[0]);
		kai2=calc_kai2(kimu,real);
		
		printf("kai2:%f\n",kai2);
		for(i=0;i<TIMES;i++){
			gennum(COUNT,kimu_prob,gen);
			kai2s[i]=calc_kai2(kimu,gen);
			//printf("%f\n",kai2s[i]);
		}
		bigger_cnt=0;
		for(i=0;i<TIMES;i++){
			if(kai2<kai2s[i]){
				bigger_cnt++;
			}
		}
		prob_big=(double)(bigger_cnt)/TIMES;
		printf("prob_big:%f\n",prob_big);
		
		return 0;
	}
	
	double calc_kai2(double kimu[4],int dat[4]){
		int i;
		double kai2;
		kai2=0;
		for(i=0;i<4;i++){
			kai2+=(dat[i]-kimu[i])*(dat[i]-kimu[i])/kimu[i];
		}
		return kai2;
	}
	
	void gennum(int cnt,double kimu_prob[4],int gen[4]){
		int i,j,chk;
		double conv,rnum;
		for(i=0;i<4;i++){
			gen[i]=0;
		}
		for(i=0;i<cnt;i++){
			rnum=genrand_close_open();
			conv=0;
			for(j=0;j<4;j++){
				conv+=kimu_prob[j];
				if(rnum<conv){
					gen[j]++;
					//printf("%d\t%d\t%f\t%f\n",i,j,rnum,conv);
					break;
				}
				if(j==3){
					//ありえない場合
					printf("error:%d\t%d\t%f\t%f\n",i,j,rnum,conv);
				}
			}
		}
		chk=0;
		for(j=0;j<4;j++){
			chk+=gen[j];
		}
		if(chk!=cnt){
			//ありえない場合
			printf("error:%d\t",chk);
		}
	}

尤度について

L=41!/(a!b!c!d!) *(a/n)^a*(b/n)^b*(c/n)^c*(d/n)^d

とした式をカイ二乗統計量の代わりに用いる。

後はif文中の kai2>kai2s を \lambda=（定数）と設定し、 \lambdaを調整して（多分\lambda=1でいいと思います） (\lambda)*kai2<kai2s　とすれば尤度のほうもできると思われます。

導出過程は添付ファイルを見てください。
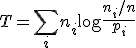
そ、そうなの？…尤度比検定統計量 $T = \sum_{i}n_{i}\log \frac{n_{i}/n}{p_i}$
を使えばいいのでは?それとも

L=41!/(a!b!c!d!) *(Pa)^a*(Po)^b*(Pb)^c*(Pab)^d

ならかなり近い値になるかも？ by tako

カイ二乗適合度検定の例 のバックアップ(No.3)

概要 †

実際 †

カイ二乗適合度検定の例のバックアップ(No.3)