![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
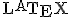 の練習
の練習
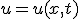
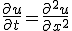
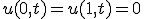
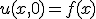
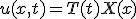 という形の解を仮定すると
という形の解を仮定すると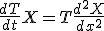 を満たす。
を満たす。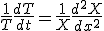
 に依存せず、右辺は
に依存せず、右辺は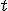 に依存しないので、両辺は定数でなければならない。
に依存しないので、両辺は定数でなければならない。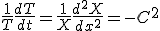
 の方を解くと。
の方を解くと。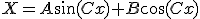
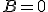 ~、
~、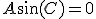
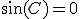 、
、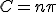 のときのみ存在し、
のときのみ存在し、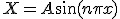
 の方を解くと、
の方を解くと、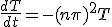
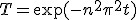
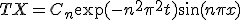
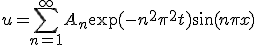
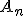 を決めれば最終的な解が求まる。
を決めれば最終的な解が求まる。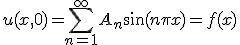

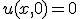 、
、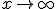 で
で が有界、にする。
が有界、にする。 の方を解くと、
の方を解くと、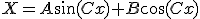
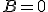 、
、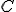 は任意の実数でよい。
は任意の実数でよい。 の方も解いてから重ね合わせると、
の方も解いてから重ね合わせると、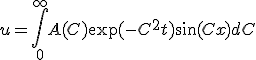
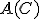 を決めると、
を決めると、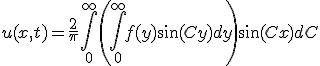
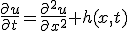 とする。他の条件は同じ。
とする。他の条件は同じ。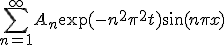 を少し一般化して、
を少し一般化して、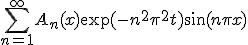 の形で探してみる。
の形で探してみる。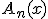 が満たすべき方程式は、
が満たすべき方程式は、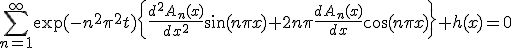
 化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば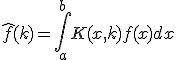 という形の関数から関数への線形変換を積分変換と呼ぶ。
という形の関数から関数への線形変換を積分変換と呼ぶ。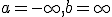
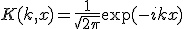 と選び、~
と選び、~