![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![F\left(\{x_i\}_{i=1}^{n};\{t_i\}_{i=1}^{n}\right) = P[\{X_{i}(t_i) \leq x_i \}_{i=1}^{n}]](./cache/f6e3fc2fd2d61ce6659f448e4b984793.mimetex.gif)
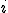 番目の値が時刻
番目の値が時刻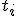 に
に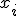 以下である確率。
以下である確率。![\eta(t) = E[x(t)] = \int_{-\infty}^{\infty}x f(x,t)dx](./cache/0a0940f0f268936457a5dc19350ac9d7.mimetex.gif)
![R(t_1,t_2) = E[x(t_1)x(t_2)]](./cache/3660c4edbff1c5bd6dac3c20dbc05264.mimetex.gif)
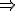 無相関
無相関ここに間違えがあったとしても私は責任を負えません.
責任はtzikにあります.
誤植は見つけた人が直すものです.
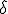 関数
関数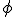 に対し
に対し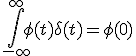 が成立するような関数.
が成立するような関数.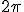 倍したもの.
倍したもの.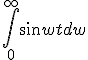 を求めよ.
を求めよ.![\begin{align}\int_0^{\infty}\sin wt dw&=\left[\frac{-\cos wt}{w}\right]_0^{\infty}\\ &=\frac{1}{t}\end{align}](./cache/86fc1cc9f940ae777e0d82773b7a9165.mimetex.gif)
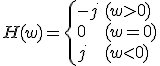 の逆Fourier変換を求めよ.
の逆Fourier変換を求めよ.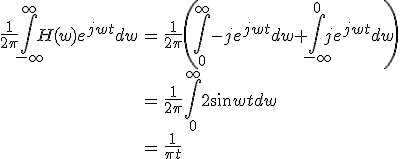
 で定義される変換はHilbert変換と呼ぶか?また,実信号
で定義される変換はHilbert変換と呼ぶか?また,実信号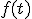 に対し,
に対し,
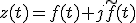
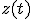 の性質を述べよ.
の性質を述べよ.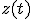 は解析信号と呼ばれ,
は解析信号と呼ばれ,
![\mathcal{F}[z(t)]=2F(w)U(w)](./cache/5580014949e3b07b7e4c6f6b00cb8d60.mimetex.gif) が成り立つ.
が成り立つ.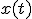 を実数値をとる定常過程とし,
を実数値をとる定常過程とし,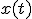 の自己相関関数を
の自己相関関数を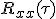 と表すとき,以下の問いに答えよ.
と表すとき,以下の問いに答えよ.
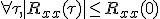 ?
?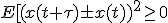 より
より
![E[(x(t+\tau))^2]\pm 2E[x(t+\tau)x(t)]+E[(x(t))^2]\ge 0](./cache/209cd0e1e0b906782adb1e06f11fffa3.mimetex.gif) なので,
なので,
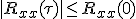
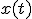 のパワースペクトル
のパワースペクトル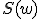 を,
有限の観測時間
を,
有限の観測時間![[-T,T]](./cache/02da93263c04f4457d5fd107598aa2dc.mimetex.gif) から推定するための式は?
から推定するための式は?![\mathcal{F}[\frac{1}{2T}\int_{-T}^{T}x(t-\tau)x^*(t)dt]](./cache/b79d8f7969fd9a20d696071e1e98637f.mimetex.gif)
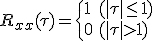 となるような定常過程って何?
となるような定常過程って何?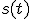 に雑音
に雑音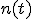 が重畳した
が重畳した
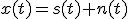 が観測信号として得られるものとする.
ただし,
が観測信号として得られるものとする.
ただし,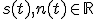 で,
互いに無相関な定常過程であり,それぞれのパワースペクトルは,
で,
互いに無相関な定常過程であり,それぞれのパワースペクトルは,
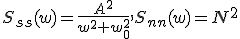
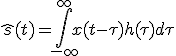
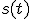 の推定値
の推定値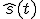 を得る時,
誤差の二乗平均
を得る時,
誤差の二乗平均![J=E[(s(t)-\hat{s}(t))^2]](./cache/2afe384c94925c6323f04390a07f9e10.mimetex.gif) を最小とするような
線形フィルタ
を最小とするような
線形フィルタ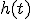 をWiener Filterと呼ぶ.
をWiener Filterと呼ぶ.
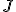 を最小とする
を最小とする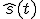 は
は
![E[(s(t)-\hat{s}(t))x(t-\tau)]=0](./cache/d7e843c184a8b9bb77bed47314417812.mimetex.gif)
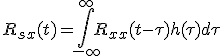
![\begin{align}R_{xx}(t)&=E[s(\tau)x(\tau-t)]\\&=E[\hat{s}(\tau)x(\tau-t)]\\&=E[x(\tau-t)\int_{-\infty}^{\infty}x(\tau-\tau ')h(t)d\tau ']\\&=\int_{-\infty}^{\infty}E[x(\tau-t)x(\tau-\tau ')]h(\tau ')d\tau '\\&=\int_{-\infty}^{\infty} R_{xx}(t-\tau ')h(\tau ')d\tau '\\&=\int_{-\infty}^{\infty}R_{xx}(t-\tau)h(\tau)d\tau\end{align*}](./cache/ad2d3dd018dcac536e65b508a93f24c4.mimetex.gif)
 の周波数応答は?
の周波数応答は?![R_{xx}=E[(s+n)^2]=R_{ss}+R_{nn}](./cache/e31d0722fb70de68751a24ff72eddf98.mimetex.gif)
![R_{sx}=E[s(s+n)]=R_{ss}](./cache/1b3854b316964f78ba10dbaa474eacaf.mimetex.gif)
![S_{sx}(w)=S_{xx}(t)\cdot \mathcal{F}[h(t)]](./cache/982a1a66f5fa8431d79609c03ca56b46.mimetex.gif)
![\begin{align}\mathcal{F}[h(t)]&=\frac{S_{sx}(w)}{S_{xx}(w)}\\&=\frac{A^2}{A^2+N^2(w^2+w_0^2)}\end{align}](./cache/122ce04b7eee0978e88cc6b3ab1f549a.mimetex.gif)