講義日程-2007年度冬学期
幾何数理工学 †
- 担当:増田 直紀 講師
- 1.5単位
- 8:30-10:00 工学部六号館 62講義室
- レポート1~2回、中間試験、期末試験
内容 †
- 幾何学(Geometry)~~様々な図形を一定の視点の下で眺め、これらの図形の性質を研究。~~一定の視点とは、何らかの変換。図形の性質とは、その変換で不変な性質。
- 位相幾何学(Topology):位相同型変換によって不変な位相空間の性質を扱う。
- テンソルの幾何学:座標変換(C^∞級同型)によって不変な多様体の性質?
- トポロジー
- ユークリッド幾何学(Euclidean Geometry)~~合同変換(Congrument Transformation)によって不変な図形の幾何学。~~合同変換:二点間の距離を変えない変換。(平行移動・回転・鏡映とその合成)~~長さ・角度・面積などが不変量。
- 位相幾何学(Topological Geometry)~~位相同型写像で~~位相同型写像:連続な全単射で逆写像も同型なもの。~~長さ・角度・面積などは変化する。~~図形のつながり方が不変。図形に空いた穴や図形のねじれ、境界の開・閉。~~伸縮させて同じ形にできる図形は同じものとみなす。~~コーヒーカップとドーナツは位相同型。
- 距離空間(Metric Space):距離関数の備わった集合。
- 距離関数:三角不等式を満たす、非負で対称な二変数関数で、密着でないもの。
- 距離空間X,Yについて、~~ {a[n]}_{n∈N}~~lim[x→∞]a[n]=a~~⇔(∀ε>0.∃n∈N.∀m>n⇒d(a[m],a)<ε)で極限を定義し、~~f:X→Yについて、Xの任意の収束列{x[n]}について~~lim[n→∞]f(x[n])=f(lim[n→∞]x[n])ならばfは連続と定義する。~~∀ε>0.∃δ>0. ∀x,y∈X. d(x,y)<δ⇒d(f(x),f(y))<ε~~∀x∈X.∀ε>0.∃δ>0. f(N(x,δ))⊂N(f(x),ε)~~も同値。
- 連続でない写像で図形を変換すると、片方の空間で収束するものがもう片方では収束しない場合がある。~~図形が破れている。
- 単射でない写像を使うと、異なる二点を同じ点に移すので、図形を張り合わせてしまっている。
- 逆写像が連続でない全単射では、境界の開の部分と閉の部分を張り合わせる場合が残っている。
- 位相空間(Topological Space):位相の備わった集合。距離空間の一般化。
- 位相:連続写像や極限を定義するための仕組み。
- 開集合系:有限積と加算和について閉じた集合族。~~この集合族に属する集合を「開集合」とみなし、開集合の逆像が開集合になるような写像が連続写像。
- 閉集合系:有限和と加算積について閉じた集合族。~~開集合系と同様に位相を定める。
- 近傍系:
- 閉包作用素:部分集合から部分集合への写像で、空を空に移し、合併とついて分配でき、冪等で拡大なもの。
- 位相同型写像:連続な全単射で逆写像も連続なもの。~~「切り取らず」(連続)~~貼り付けず(単射)、変形を許す写像(全射)。
- 距離空間の位相
- 距離空間X中の部分集合Aの点xについて、~~Xに含まれるx周りの開球が存在すれば、xはAの内点。~~存在しなければxはAの外点。~~Aの外点全体を∂Aと書き、∂AをAの境界と呼ぶ。~~(多様体の境界とは別物。)
- 開集合・閉集合の定義、その1
- 境界と交わりの無い集合が開集合。
- 境界を含む集合が閉集合。
- 開集合の補集合は閉集合。~~閉集合の補集合は開集合。~~空間と全体は開かつ閉な集合。~~開でも閉でも無い集合もある。
- 開集合・閉集合の定義、その2~~距離空間Xの部分集合Aについて
- A中の任意の点について、その点まわりの開球が存在すれば、Aは開集合。
- Aの補集合が開集合ならAは閉集合。
- この二種類の定義は同値だが、後者の方が位相空間に一般化しやすい。
- この開集合・閉集合の定義は距離に依存する。~~例えば離散距離を入れれば任意のの部分集合は開かつ閉になる。
- 連続写像
- 距離空間X,Yとf:X→Yについて、次の3つは同値
- fが連続(⇔∀x∈X.∀U∈N(f(x))).∃V∈N(x). s.t. f(V)⊂U)
- Yの任意の開集合の逆像はXの開集合。~~連続写像は開写像とは限らない。開を開へ移すとは限らない。
- Yの任意の閉集合の逆像はXの閉集合。
- 開集合・閉集合を距離に依存しない形で定義してやれば、~~距離に依存せずに写像の連続性を定義できる。
- 「f:X→Yが位相同型写像」⇔「fは全単射で連続な開写像」
- 開集合の公理
- 距離空間Xの開集合全体をOとすると、Oは以下の開集合の公理を満たす。
- φ∈O, X∈O
- U,V∈O ⇒ U∩V∈O ~~(二つについて言えば再帰的に有限個について言った事になる)~~∀x∈U∩V⇒∃α>0.∃β>0.N(x,α)⊂U∧N(x,β)⊂V⇒N(x,min(α,β))⊂U∩V
- {O[i]}_(i∈I). O[i]∈O. について、∪[i∈I]O[i] ∈ O~~(Iの濃度については言及していない。任意の濃度でよい)~~∀x∈∪[i∈I]O[i].∃i∈I.x∈O[i]⇒∃ε>0.N(x,ε)⊂O[i]⊂∪[i∈I]O[i]
- 閉集合の公理
- 距離空間Xの閉集合全体をFとすると、Fは以下の閉集合の公理を満たす。
- φ∈F, X∈F
- U,V∈F ⇒ U∪V∈F
- {O[i]}_(i∈I). O[i]∈O. について、∩[i∈I]O[i] ∈ O
- 補)集合論から
- 任意の集合Aについて、その部分集合全体は集合を成すと見なし、それを2^Aと表す。(冪集合の公理)
- 集合A,Bについて、AからBへの写像全体は集合を成し、B^Aと書く。~~2={0,1}と見ると、冪集合2^AはAから2への写像全体と同型。
- 位相空間~~必ずしも距離の入っていない集合について、開集合の公理を満たすように人工的に開集合を指定する。
- 開集合による位相
- 集合Xについて、開集合の公理を満たすXの部分集合族Tを、開集合系によるXの位相と呼び、位相を伴った集合(X,T)を位相空間と呼ぶ。~~毎回ペアで書くのは面倒なので、どの位相を入れているか明らかなときにはTは省略されることが多い。~~Tは一意には定まらない。位相の入れ方は複数考えられる。~~位相には包含関係による順序づけができる。~~開集合系による位相の定義以外にも閉集合系・近傍系・閉包作用素・開核作用素などでも位相を定義できる。~~どれが一つで定義すればそこからほかのも定義できる。
- 位相空間(X,T)について、開集合系に含まれる集合を開集合。開集合の補集合を閉集合と呼ぶ。
- 最も弱い位相として密着位相{φ,X},最も強い位相として離散位相2^Xがある。
- 連続写像
- 位相空間 X,Y 間の写像 f:X→Y について、~~fが連続であるとは、Yの任意の開集合の逆像がXの開集合であること。
- fが開写像であるとは、任意のXの開集合の像がYの開集合であること。
- 位相同型写像
- 位相空間の間の連続で全単射な開写像を位相同型写像・同相写像であるという。
- 二つの位相空間の間に位相同型写像が存在するとき、その位相空間は互いに同相であるという。
- 近傍系
- 位相空間X上の点xについて、xを含む開集合を開近傍。xの開近傍を含む集合を近傍と呼び、その全体をN(x)と表す。
- 「xを内点のとして含む集合」や「開核がxを含む集合」としても同値。
- AがXの開集合であることと、A上の任意の点についてAに含まれる近傍が存在することは同値。
- AがXの閉集合であることと、A^C上の任意の点についてAと交わらない近傍が存在することは同値。
- 位相空間X,Yについて、f:X→YがX上の点xにおいて連続であるとは、Yにおけるf(x)の任意の近傍Vについて、f(U)⊂Vとなるxの近傍Uが存在すること。~~fがX上の任意の点で連続ならば、fはX全体で連続。
- 距離空間と位相空間
- 距離空間は距離に伴う通常の開集合系を使って位相を定められる。~~特に(R^n,d_2)の位相をEuclid位相と呼ぶ。
- 連結性
- 開かつ閉な集合が全体と空集合以外になければ連結。
- 空でない互いに疎な開集合で全空間を分割できるなら不連結。
- コンパクト性
- ある集合族で集合を覆えるとき、その集合族を被覆という。
- 被覆に含まれる集合が全部開集合なら開被覆という。
- 開被覆の要素の数が有限なら有限開被覆という。
- 要素数を指定しない任意の開被覆から、有限開被覆を選び出せるとき、その集合はコンパクトだという。
- ユークリッド空間については、コンパクトであることと有界閉集合であることは同値。
- 直和分割
- 全空間を互いに疎な集合族に分割すること。
- 同値関係で同値類を作ると、同値類全部を集めたものは直和分割。
同値類による分割を分類と呼び、同値類全体の集合を商集合と呼ぶ。
集合の要素から、その要素が属する同値類への写像を標準全射と呼ぶ。
- 路,道,弧,パス
- 位相空間
 と任意の2点
と任意の2点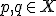 に対して、
に対して、
連続写像![f:[0,1]\to X](./cache/88b85fbd9cd7c1be650daf613bd6ab08.mimetex.gif) で
で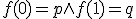 となるものをpからqへの路という。
となるものをpからqへの路という。
- 弧状連結
- 空間上の任意の2点について、それらを結ぶ路が存在すること。
- 弧状連結ならば連結。
- 路の変形,ホモトープ,ホモトピー
- 位相空間
 上の2点
上の2点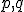 と
と
それらを結ぶ2つの路![f,g : [0,1]\to X](./cache/2e6d132f2126f51e4595ce3bd5a20a9d.mimetex.gif) について、
について、
「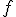 が
が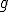 に変形できる」とは、
に変形できる」とは、
連続写像![F:[0,1]\times [0,1] \to X](./cache/d08fb0daf6267de7ce61c361a1b048b9.mimetex.gif) で、
で、
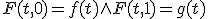 が存在するとき、
が存在するとき、
fはgに変形できる、と言い、Fはfからgへのホモトピーと呼び、
fとgは互いにホモトープと言う。
ホモトープであることは同値関係。
(空間上の2点を固定して)空間上の曲線をホモトープによる同値関係で分類できる。
- ホモトープによる同値類の数は位相不変量(同相写像によって変わらない性質。)
この商集合は有限集合になるとは限らず、扱いが難しい。
商集合に適当な演算を定義して群を作り、代数的な構造から元の空間の性質を調べる。
- 基本群
- 位相空間X上に基点pを決めたとき、基本群
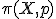 は
は
pを通る連続閉曲線をホモトープによる同値関係で割ったもの。
- 単体
位相空間上のm単体は、空間上の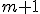 点を相互に交わらない曲線で結んだもの。
点を相互に交わらない曲線で結んだもの。
単体の辺は、m単体を構成する点から、任意にm個点を選んで作られた(m-1)単体。
点・線分・三角形・正四面体など、図形を構成するための基本図形。
- 複体
有限個の単体の集合 が複体であるとは、
が複体であるとは、
 に含まれる任意の単体の任意の辺が
に含まれる任意の単体の任意の辺が に含まれ、
に含まれ、
 に含まれる任意の2つの単体の共通部分は、空であるか
に含まれる任意の2つの単体の共通部分は、空であるか にふくまれること。
にふくまれること。
異なる複数の複体が同一の図形を表すこともある。
図形を単体に分割する方法は一つには決まらない。
- 単体写像
複体Kから複体Lへの写像で、Kに含まれる単体を
Lに含まれる単体に移す写像を単体写像と呼ぶ。
特に全単射な単体写像を単体同型写像と呼び、
単体同型写像が存在する2つの複体は、単体同型であるという。
単体同型な複体が表す多面体は、互いに位相同型になる。
- 細分
多面体として等しい2つの複体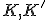 で、
で、
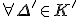 に対して
に対して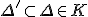 となるとき、
となるとき、
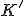 は
は の細分であるという。
の細分であるという。
- 組み合わせ同型
2つの複体に、それぞれの細分に単体同型となるものがあれば
その2つの単体は組み合わせ同型と呼ばれる。
- 記法
- 位相同型、
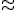 、位相空間同士に連続で開写像な全単射がある。
、位相空間同士に連続で開写像な全単射がある。
- 同値、
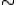 、反射律・対称律・推移律を満たす2項関係。
、反射律・対称律・推移律を満たす2項関係。
- ホモトープ同値、
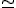 、位相空間上の曲線が連続的に移り変われること。
、位相空間上の曲線が連続的に移り変われること。
- 群の同型、
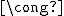 、群同士に群演算と両立する全単射があること。
、群同士に群演算と両立する全単射があること。
- 単体同型、
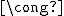 、複体同士に構造を保つ全単射があること。
、複体同士に構造を保つ全単射があること。
- 組み合わせ同型、
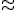 、複体同士が、単体同型な細分を持つこと。
、複体同士が、単体同型な細分を持つこと。
- 組み合わせ的にホモトープ、
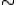 、折れ線同士が初等変形で移り変われる。
、折れ線同士が初等変形で移り変われる。
基本群を定義から直接求めて、同型かどうかを調べるのは難しい、
位相空間に複体構造を入れて、折れ線群を定義できると、計算が容易になる。
- 複体上の折れ線
複体上の1単体を連ねたものを、複体上の折れ線と呼ぶ。
- 折れ線の積
複体 上の2つの折れ線
上の2つの折れ線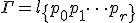
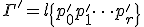 で、
で、
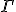 の終点
の終点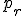 と
と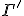 の始点
の始点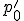 が一致するとき、
が一致するとき、
2つの折れ線に積が定義でき、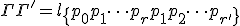
と折れ線を繋いだものを積とする。
- 折れ線の初等変形
以下の操作とその逆を折れ線の初等変形という。
- 同じ点が2つ続いたら、1つを除くこと。
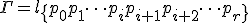
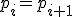
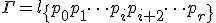
- 同じ点に挟まれた点を除くこと、
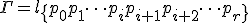
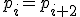
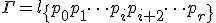
- 連続する3つの点からなる単体がもとの複体に含まれるとき、
中間の点を除くこと。
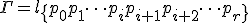
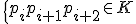
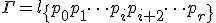
- 組み合わせ的にホモトープ、折れ線同値
始点と終点が一致する二つの折れ線が、初等変形で移り変われるとき、
その2つの折れ線は組み合わせ的にホモトープという。
- 折れ線群
複体上に基点を1つ選び、その点を通る閉折れ線を
組み合わせホモトピーの同値関係で割ったものは
折れ線の連結について群になり、それを複体上の折れ線群と呼ぶ。
複体の折れ線群と、複体が構成する多面体の基本群は群として同型。
- ホモロジー
閉曲線による切断に注目する。
例えばトーラスをループで切断するとき、
トーラスを二つの部分に分割するループと
分割しないループがある。
球面上でなら、どのループで切断しても二つの部分に分かれる。
- 単体の向き
多角形として同じ単体が同じ向きであるとは、単体をなす点の列が互いに偶置換で移り変われること。
逆向きであるとは、奇置換で移り変われること。
- 凖同型定理
2つの群の間の凖同型写像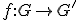 について、
について、
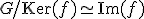
- ホモロジー群
- 複体
 の
の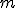 次元サイクル:
次元サイクル: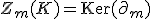
- 複体
 の
の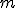 次元境界サイクル:
次元境界サイクル: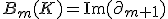
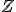 は切断を表す
は切断を表す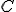 の部分群。
の部分群。
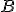 は図形を分ける切断を表す
は図形を分ける切断を表す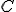 の部分群。
の部分群。
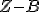 が図形を分けない切断を表している。
が図形を分けない切断を表している。
境界サイクル分の違いを無視して、
ホモロジー群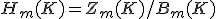 を作れば複体の穴の状態を反映した群ができあがる。
を作れば複体の穴の状態を反映した群ができあがる。
- ホモローグ
2つの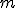 次元サイクル
次元サイクル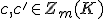 がホモローグであるとは、
がホモローグであるとは、
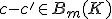 であること。
であること。
ホモローグは同値関係。ホモローグによる同値類はホモロジー類と呼ばれる。
- 来週は中間テスト。持ち込み可。折れ線まで。印刷物は50枚まで。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
 と任意の2点
と任意の2点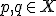 に対して、
に対して、![f:[0,1]\to X](./cache/88b85fbd9cd7c1be650daf613bd6ab08.mimetex.gif) で
で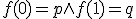 となるものをpからqへの路という。
となるものをpからqへの路という。 上の2点
上の2点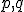 と
と![f,g : [0,1]\to X](./cache/2e6d132f2126f51e4595ce3bd5a20a9d.mimetex.gif) について、
について、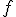 が
が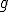 に変形できる」とは、
に変形できる」とは、![F:[0,1]\times [0,1] \to X](./cache/d08fb0daf6267de7ce61c361a1b048b9.mimetex.gif) で、
で、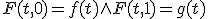 が存在するとき、
が存在するとき、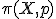 は
は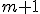 点を相互に交わらない曲線で結んだもの。
点を相互に交わらない曲線で結んだもの。 が複体であるとは、
が複体であるとは、 に含まれる任意の単体の任意の辺が
に含まれる任意の単体の任意の辺が に含まれ、
に含まれ、 に含まれる任意の2つの単体の共通部分は、空であるか
に含まれる任意の2つの単体の共通部分は、空であるか にふくまれること。
にふくまれること。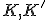 で、
で、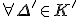 に対して
に対して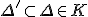 となるとき、
となるとき、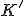 は
は の細分であるという。
の細分であるという。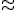 、位相空間同士に連続で開写像な全単射がある。
、位相空間同士に連続で開写像な全単射がある。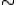 、反射律・対称律・推移律を満たす2項関係。
、反射律・対称律・推移律を満たす2項関係。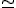 、位相空間上の曲線が連続的に移り変われること。
、位相空間上の曲線が連続的に移り変われること。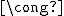 、群同士に群演算と両立する全単射があること。
、群同士に群演算と両立する全単射があること。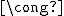 、複体同士に構造を保つ全単射があること。
、複体同士に構造を保つ全単射があること。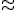 、複体同士が、単体同型な細分を持つこと。
、複体同士が、単体同型な細分を持つこと。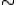 、折れ線同士が初等変形で移り変われる。
、折れ線同士が初等変形で移り変われる。 上の2つの折れ線
上の2つの折れ線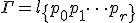
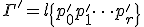 で、
で、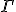 の終点
の終点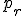 と
と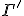 の始点
の始点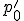 が一致するとき、
が一致するとき、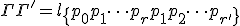
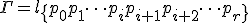
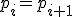
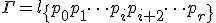
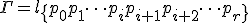
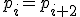
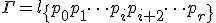
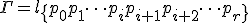
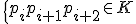
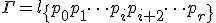
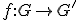 について、
について、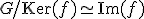
 の
の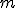 次元サイクル:
次元サイクル: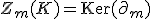
 の
の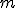 次元境界サイクル:
次元境界サイクル: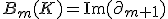
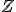 は切断を表す
は切断を表す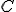 の部分群。
の部分群。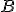 は図形を分ける切断を表す
は図形を分ける切断を表す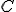 の部分群。
の部分群。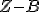 が図形を分けない切断を表している。
が図形を分けない切断を表している。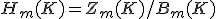 を作れば複体の穴の状態を反映した群ができあがる。
を作れば複体の穴の状態を反映した群ができあがる。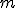 次元サイクル
次元サイクル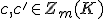 がホモローグであるとは、
がホモローグであるとは、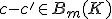 であること。
であること。