![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
担当:谷口(やぐち)さん
yaguchi@mist.i.(東大ドメイン) 6号館356号室
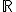 への写像。
への写像。
 上の点
上の点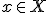 に対して、
に対して、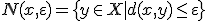
 の
の 近傍と呼ぶ。
近傍と呼ぶ。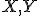 について、写像
について、写像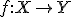 が
が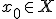 で連続であるとは、
で連続であるとは、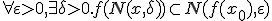 となること。
となること。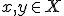 を繋ぐ連続曲線とは、
を繋ぐ連続曲線とは、![f:[0,1]\to X](./cache/88b85fbd9cd7c1be650daf613bd6ab08.mimetex.gif) で
で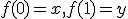 を満たす連続写像。
を満たす連続写像。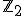 上で考え、2重になった辺を排除
上で考え、2重になった辺を排除 の
の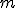 次元鎖群
次元鎖群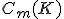
 に含まれる
に含まれる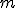 単体に
単体に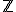 を係数につけて
を係数につけて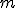 単体
単体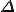 の境界、
の境界、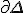 は、
は、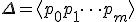
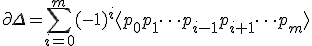 で定義する。
で定義する。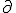 は境界作用素,境界準同型と呼ばれる。
は境界作用素,境界準同型と呼ばれる。 に
に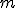 次元輪体群
次元輪体群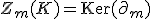 、(
、(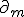 は
は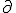 の定義域をm単体に限ったもの。)
の定義域をm単体に限ったもの。) のm次元境界輪体群
のm次元境界輪体群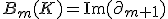
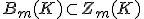 が成立。
が成立。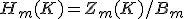 を調べると、図形の「穴」の状態がわかる。
を調べると、図形の「穴」の状態がわかる。 の
の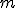 次元ホモロジー群と呼ぶ。
次元ホモロジー群と呼ぶ。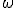 と、外微分作用素も同じ関係を持つ。
と、外微分作用素も同じ関係を持つ。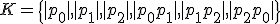 について、
について、![C_{0}(K) = \mathbb{Z}[\langle p_0 \rangle,\langle p_1 \rangle,\langle p_2 \rangle]](./cache/f53cd35d50dae19c5e618ca94492e494.mimetex.gif)
![C_{1}(K) = \mathbb{Z}[\langle p_{0}p_{1} \rangle,\langle p_{1}p_{2} \rangle,\langle p_{2}p_{0} \rangle]](./cache/9347b96e50522239de060bbd48665bbf.mimetex.gif)
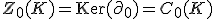
![Z_{1}(K) = \mathrm{Ker}(\partial_1) = \mathbb{Z}[\langle p_{0}p_{1} \rangle + \langle p_{1}p_{2} \rangle + c \langle p_{2}p_{0} \rangle]](./cache/56fab1060a0d511ee8be6ab2c25ed8e8.mimetex.gif)
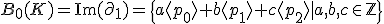
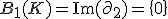
![H_{0}(K) = Z_{0} / B_{0} = \mathbb{Z}[\langle p_2 \rangle ]](./cache/281fe356c800775e07a6b814078a1ea3.mimetex.gif)