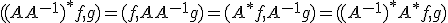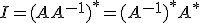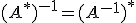![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
 で定義された2乗可積分の空間
で定義された2乗可積分の空間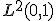 は無限次元であることを示せ。
は無限次元であることを示せ。
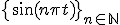 が直交無限列。証明略。
が直交無限列。証明略。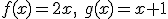 とする。
とする。
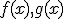 が
が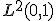 の元であることを示せ。
の元であることを示せ。
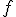 のノルム
のノルム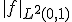 を求めよ。
を求めよ。
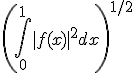 を計算。値は
を計算。値は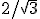
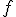 と
と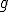 の内積
の内積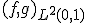 を計算せよ。
を計算せよ。
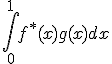 を計算。値は
を計算。値は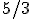
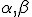 を
を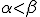 なる実数とし、閉区間
なる実数とし、閉区間![I=[\alpha,\beta]](./cache/d309337bf41c121fb3946a220c29dc1b.mimetex.gif) を考える。
を考える。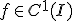 に対して
に対して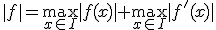
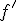 は
は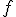 の導関数を表す。
の導関数を表す。
 は
は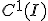 のノルムであることを示せ。
のノルムであることを示せ。
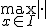 についての三角不等式から。
についての三角不等式から。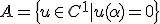 は
は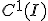 の閉部分空間であることを示せ。
の閉部分空間であることを示せ。
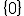 は
は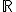 の閉集合なので、
の閉集合なので、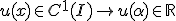 が連続写像であることを示せばよい。
が連続写像であることを示せばよい。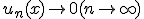 となる
となる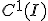 の列について、
の列について、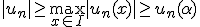 から
から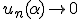 よってこの写像は連続。
よってこの写像は連続。 は閉集合。
は閉集合。 で
で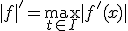
 と
と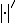 とは同値であることを示せ。
とは同値であることを示せ。
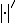 がノルムになっていることの証明は略。
がノルムになっていることの証明は略。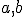 をとって、
をとって、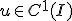 について
について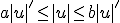 を成立させることができればよい。
を成立させることができればよい。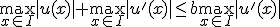 を示す。
を示す。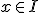 に対してある
に対してある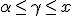 が存在し、
が存在し、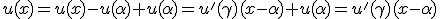 が成立。
が成立。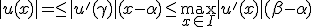
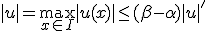
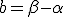 とすればよい。
とすればよい。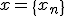 全体を数列空間と呼び、
全体を数列空間と呼び、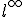 と書き表す。
と書き表す。
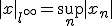 は
は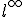 のノルムであることを示せ。
のノルムであることを示せ。
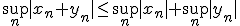 を示す。
を示す。 について、ある
について、ある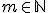 が存在し、
が存在し、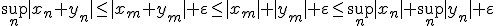
 は任意に小さくできるので、
は任意に小さくできるので、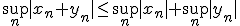 が成立。
が成立。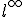 がバナッハ空間であることを示せ。
がバナッハ空間であることを示せ。
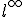 の任意のコーシー列
の任意のコーシー列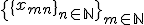 について、
について、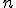 を固定した
を固定した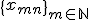 もコーシー列になることを示せば
もコーシー列になることを示せば に対して、ある
に対して、ある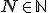 が存在し、
が存在し、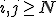 について
について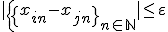 が成立する。
が成立する。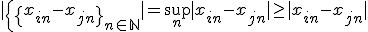 なので
なので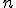 を任意に固定した個々の
を任意に固定した個々の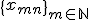 もコーシー列で、収束先
もコーシー列で、収束先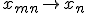 、
、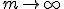 が存在する。
が存在する。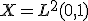 とする。
とする。
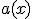 を、
を、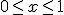 で連続な関数とし、線形作用素
で連続な関数とし、線形作用素 を
を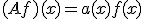
![D(A) = A^{-1}[X]](./cache/94db3a0f6c0ab69b3fdce429b8fc8a7c.mimetex.gif) とする。
とする。 は有界作用素、すなわち連続作用素であることを示せ。
は有界作用素、すなわち連続作用素であることを示せ。
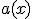 は有界閉区間で連続なので有界。最大値が存在する。
は有界閉区間で連続なので有界。最大値が存在する。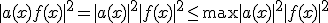
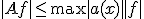
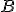 を
を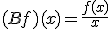
![D(B)= B^{-1}[X]](./cache/6b51d8741bc771863197664038c67057.mimetex.gif) と定義する。
と定義する。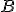 は有界作用素ではないことを、関数列
は有界作用素ではないことを、関数列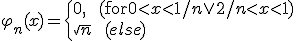
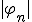 および
および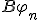 を計算して示せ。
を計算して示せ。
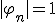 、
、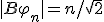
 をヒルベルト空間とする。線形作用素
をヒルベルト空間とする。線形作用素 およびその逆作用素
およびその逆作用素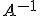 が有界作用素であれば、
が有界作用素であれば、 の共役作用素
の共役作用素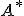 について、
について、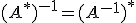 であることを示せ。
であることを示せ。
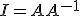
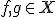 について、
について、