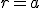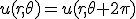講義日程-2007年度冬学期
数理手法Ⅱ †
- 担当:河村 哲也 非常勤講師(お茶の水女子大学教授)
- 1.5単位
- 物工:限定選択
- 数理:限定選択B
- システム:限定選択※
- 16:30-18:00 工学部六号館 63講義室
- 教科書
内容 †
- 偏微分方程式の数値解法とその応用
- 大部分の偏微分方程式は解析的には解けない→数値的に解く。
- 物理法則に現れる偏微分方程式の多くは2階。
線形なものの方が解きやすい。非線形なものはできる範囲で線形化。
- 数理物理学に現れる偏微分方程式(PDE,Partial Differential Equation)
⇔常微分方程式(ODE,Ordinal Differential Equation)
- 二つ以上の独立変数に対する偏微分を含んだ方程式。
- ラグランジュの偏微分方程式
u = u(x,y) は未知
P,Q,Rは既知として、
P(x,y,u)∂u/∂x + Q(x,y,u)∂u/∂y = R(x,y,u)~~について、~~補助方程式、dx/P = dy/Q = du/R という連立一階常微分方程式を解き、その解~~f(x,y,z) = a~~g(x,y,u) = b を使って、~~元の方程式の一般解は、任意関数φを使ってφ(f,g) = 0となる。
- ∂u/∂x + c∂u/∂t = 0 を解く。~~dx = dt/c ∧ du = 0 ⇒ u = a ∧ t-cx=bなので、一般解は~~φ(u,t-cx)=0~~uについて解けば u = ψ(t-cx)~~x軸正の方向へ速度1/cで平行移動している。
- 一次元波動方程式~~{(∂/∂t)^2-(k∂/∂x)^2}u = 0~~微分演算を因数分解。(∂/∂t-k∂/∂x)(∂/∂t-k∂/∂x)u = 0~~ξ=x-kt, η=x+kt と変数変換すると、~~(∂/∂ξ)(∂/∂η) u = 0⇒φ(ξ) + ψ(η)が一般解。
- 二次元ラプラス方程式~~{(∂/∂x)^2 + (∂/∂y)^2}u = 0 の解は正則関数か、複素共役が正則な関数。
- 物理現象からの導出
- 弦の微小振動。弦を微小区間に分割して運動方程式を立て、弦の曲がりが小さいとして一時近似。
- 二階の準線形偏微分方程式の分類
- 拡散方程式。熱伝導方程式。熱流は等温面に垂直に、温度勾配に比例して流れると見なす。~~ある領域Ω内部の熱量変化は、(∂/∂t)∫[Ω]TdV に比例。~~領域表面からの流入量は、温度勾配の面素方向成分に比例すると考えると、∫[∂Ω]gradT dS に比例。~~この二つが比例すると見なすと、(∂/∂t)∫[Ω]TdV = a^2∫[∂Ω]gradTdS = a^2∫[Ω]ΔTdV~~これが任意の領域で成り立つので、∂T/∂t = a^2 ΔT~~比例定数a^2は、質量密度ρ、比熱c、熱伝導率κを使って a^2=κ/(ρc) と書ける。
- ポアソン方程式~~熱源ありの熱伝導方程式の平衡状態の解。~~Δu = -f~~熱源なしの場合はラプラス方程式Δu = 0
- 波動方程式、{(∂/∂t)^2 - Δ}u = 0
- 二階の準線形偏微分方程式:二階の偏微分方程式で、ニ階偏微分について一次の方程式。
- 2変数の準線形偏微分方程式、A∂[x]^2 u + B∂[x]∂[y]u + C∂[y]^2 u = Dについて、~~ξ = ξ(x,y)~~η=η(x,y)と変数変換すると、~~a = A(∂[x]ξ)^2 + B(∂[x]ξ)(∂[y]ξ) + C(∂[y]ξ)^2~~c = A(∂[x]η)^2 + B(∂[x]η)(∂[y]η) + C(∂[y]η)^2~~b = 2A(∂[x]ξ)(∂[y]η) + B{(∂[x]ξ)(∂[y]η)+(∂[y]ξ)(∂[x]η)} + 2C(∂[y]ξ)(∂[x]η)~~として、a∂[ξ]^2 u + b∂[ξ]∂[η]u + c∂[η]^2 u = dという形に変換される。~~うまくξとηを選べば、a,bを0にすることができる場合がある。~~B-4AC>0のとき、双曲型。a=c=0となるように選べる。∂[ξ]∂[η]u = fの形、もしくは(∂[ξ]^2-∂[η]^2)u = fの形にまで簡単にできる。~~B-4AC=0のとき、放物型。∂[ξ]^2 u = fの形にまで簡単にできる。~~B-4AC<0のとき、楕円型。∂[ξ]∂[ξ^*]u = fもしくは(∂[ξ]^2+∂[η]^2)u = f の形にまで簡単にできる。~~標準化した式は、いずれも右辺には一階微分までしか含まない。
- 例){y^2∂[x]^2 - 4x^2 ∂[y]^2}u = 0~~y∂[x]ξ + 2x∂[y]ξ = 0~~y∂[x]η - 2x∂[y]η = 0と変換すると、~~∂[ξ]∂[η]u = (1/(2(ξ^2-η^2)))(η∂[ξ]-ξ∂[η])u
- 偏微分方程式の解法、
 の練習
の練習
- 変数分離法
線形・同次な偏微分方程式で、境界条件も同次なときにはそのまま変数分離可能。
独立変数ごとの別々な関数の積の形で解を書いてから、境界条件を満たすような重みで重ね合わせる。
方程式や境界条件が同次でないときには、非同次の特解と同次の一般解を重ね合わせればいい。
- 有限長の一次元熱伝導
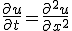
境界値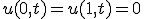
初期値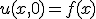
与えられた境界値条件(B.C.,Boundary Condition)と初期条件(I.C.,Initial Condition)のもとで
偏微分方程式の解を求める問題。初期値・境界値問題。
解の一意性は他で示すとして、発見的に解を見つける。
変数分離、 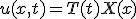 という形の解を仮定すると
という形の解を仮定すると
T,Xは、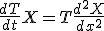 を満たす。
を満たす。
変形して、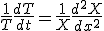
左辺は に依存せず、右辺は
に依存せず、右辺は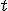 に依存しないので、両辺は定数でなければならない。
に依存しないので、両辺は定数でなければならない。
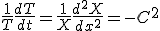
二つの別々な常微分方程式に帰着できた。
まず、 の方を解くと。
の方を解くと。
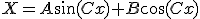
境界条件を課せば、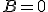 ~、
~、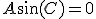
自明でない解は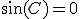 、
、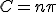 のときのみ存在し、
のときのみ存在し、
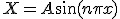
次に、 の方を解くと、
の方を解くと、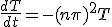
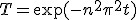
二つ合わせて、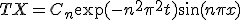
これは境界条件を満たす解の一系列になっている。
次に、元々の偏微分方程式が線形であることに注意して、初期条件を満たすために
得られた解の線形結合をとる。
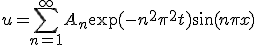
初期条件を満たすように係数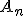 を決めれば最終的な解が求まる。
を決めれば最終的な解が求まる。
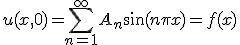

- 半無限長の一次元熱伝導
境界条件を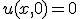 、
、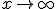 で
で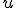 が有界、にする。
が有界、にする。
それ以外は同じ。
変数分離をして の方を解くと、
の方を解くと、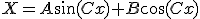
境界条件から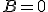 、
、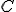 は任意の実数でよい。
は任意の実数でよい。
 の方も解いてから重ね合わせると、
の方も解いてから重ね合わせると、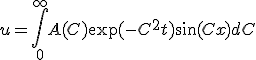
境界条件を満たすように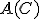 を決めると、
を決めると、
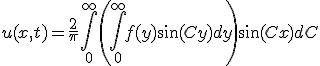
- 熱源のある有限長一次元熱伝導
熱源の無いときの偏微分方程式に項を追加して、
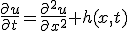 とする。他の条件は同じ。
とする。他の条件は同じ。
特解を見つけるために、定数変化法を使う。
同次方程式の解、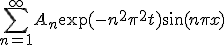 を少し一般化して、
を少し一般化して、
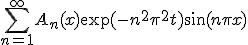 の形で探してみる。
の形で探してみる。
偏微分法定式に代入してみると。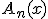 が満たすべき方程式は、
が満たすべき方程式は、
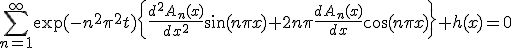
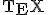 化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
非同次の一般解が得られる。
- フーリエ変換による解法
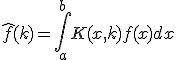 という形の関数から関数への線形変換を積分変換と呼ぶ。
という形の関数から関数への線形変換を積分変換と呼ぶ。
うまく変換すると方程式本体や境界条件を簡単にすることができる。
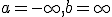
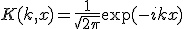 と選び、~
と選び、~
定義域を適当に設定したものをフーリエ変換と呼ぶ。
- 定義域が急減少超関数なら値域は緩増加関数。
定義域が緩増加超関数なら値域は急減少関数、などなど。少々うろ覚え。
- フーリエ変換
![\hat{f}(k) = F[f] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx](./cache/4e40dfd1bb5cd8af1bbbb6a71ef18e2a.mimetex.gif)
![f(x) = F^{-1}[\hat{f}] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{f}(k)e^{ikx}dk](./cache/2a1c4cc56c38d6c0b67b1e4653caa2af.mimetex.gif)
- 種々の公式
![F\left[\frac{d^n f}{dx^n}\right] = (ik)^{n}\hat{f}(k)](./cache/f2d727a7d520e28a127488e7945effa5.mimetex.gif)
![F[f*g] = \sqrt{2\pi}F[f]F[g]](./cache/7952637066706096cf7e8820336673fd.mimetex.gif)
![F[f\cdot g] = \frac{1}{\sqrt{2\pi}}F[f]*F[g]](./cache/cfde0161445b3d0d9bd6070d53e4f06d.mimetex.gif)
- 畳み込み
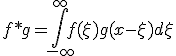
畳み込みは線形で可換、零関数以外との畳み込みは単射。
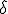 関数が単位元。
関数が単位元。
定数関数の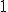 との畳み込みは全範囲での積分を表す。
との畳み込みは全範囲での積分を表す。
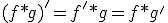
- 円形膜の振動。太鼓の中心を叩く。
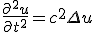
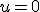 on
on 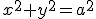
- 円筒座標系で波動方程式を解く。
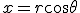
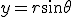
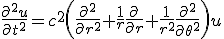
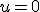 on
on 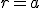
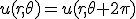
- 色々略。添付されているyambiさんのtexノート参照。
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
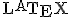 の練習
の練習
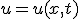
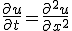
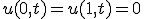
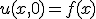
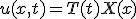 という形の解を仮定すると
という形の解を仮定すると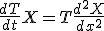 を満たす。
を満たす。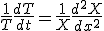
 に依存せず、右辺は
に依存せず、右辺は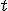 に依存しないので、両辺は定数でなければならない。
に依存しないので、両辺は定数でなければならない。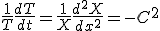
 の方を解くと。
の方を解くと。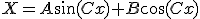
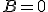 ~、
~、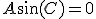
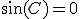 、
、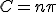 のときのみ存在し、
のときのみ存在し、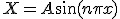
 の方を解くと、
の方を解くと、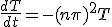
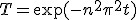
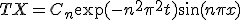
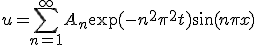
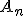 を決めれば最終的な解が求まる。
を決めれば最終的な解が求まる。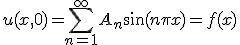

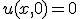 、
、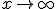 で
で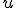 が有界、にする。
が有界、にする。 の方を解くと、
の方を解くと、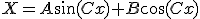
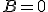 、
、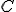 は任意の実数でよい。
は任意の実数でよい。 の方も解いてから重ね合わせると、
の方も解いてから重ね合わせると、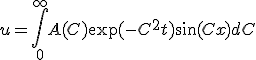
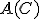 を決めると、
を決めると、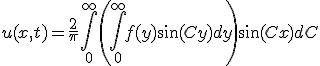
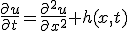 とする。他の条件は同じ。
とする。他の条件は同じ。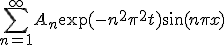 を少し一般化して、
を少し一般化して、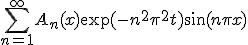 の形で探してみる。
の形で探してみる。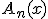 が満たすべき方程式は、
が満たすべき方程式は、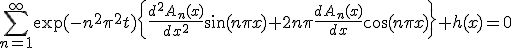
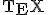 化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば
化限界により以下略。この方程式を解いて非同次の特解を求め、同次の一般解と重ね合わせれば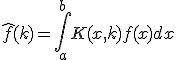 という形の関数から関数への線形変換を積分変換と呼ぶ。
という形の関数から関数への線形変換を積分変換と呼ぶ。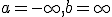
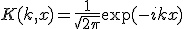 と選び、~
と選び、~![\hat{f}(k) = F[f] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-ikx}dx](./cache/4e40dfd1bb5cd8af1bbbb6a71ef18e2a.mimetex.gif)
![f(x) = F^{-1}[\hat{f}] = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\hat{f}(k)e^{ikx}dk](./cache/2a1c4cc56c38d6c0b67b1e4653caa2af.mimetex.gif)
![F\left[\frac{d^n f}{dx^n}\right] = (ik)^{n}\hat{f}(k)](./cache/f2d727a7d520e28a127488e7945effa5.mimetex.gif)
![F[f*g] = \sqrt{2\pi}F[f]F[g]](./cache/7952637066706096cf7e8820336673fd.mimetex.gif)
![F[f\cdot g] = \frac{1}{\sqrt{2\pi}}F[f]*F[g]](./cache/cfde0161445b3d0d9bd6070d53e4f06d.mimetex.gif)
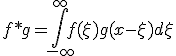
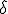 関数が単位元。
関数が単位元。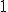 との畳み込みは全範囲での積分を表す。
との畳み込みは全範囲での積分を表す。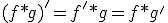
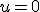 on
on 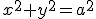
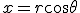
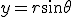
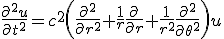
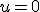 on
on