![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
これ以前は前のwikiへ
 をジョルダン標準型に
をジョルダン標準型に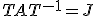 に標準化すると、
に標準化すると、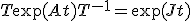
![L[\exp(Jt)] = (sI-J)^{-1}](./cache/8c913b3e4503d231d04beae52279444a.mimetex.gif)
![L[\exp(At)] = L[T^{-1}\exp(Jt)T] = T^{-1}(sI-J)^{-1} T = (sI-A)^{-1}](./cache/c0a7dd1877c3f3d84b17589175e432f1.mimetex.gif)
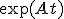 をラプラス変換すると
をラプラス変換すると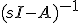
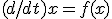 について、
について、![f(x[e]) = 0](./cache/87549c89798b0125e8e515fd9647a0a0.mimetex.gif) となる点を平衡点と呼ぶ。
となる点を平衡点と呼ぶ。 に対して、
に対して、![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が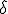 未満である初期値から時間を進めたときに、
未満である初期値から時間を進めたときに、![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) からの距離が
からの距離が 未満に留まるような正数
未満に留まるような正数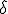 が存在するなら、その系は安定。
が存在するなら、その系は安定。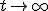 で
で![x[e]](./cache/a968e4d64bd29e698da31567c6636433.mimetex.gif) に収束するなら、その系は漸近安定であるという。
に収束するなら、その系は漸近安定であるという。![x = \exp(At)x[0]](./cache/d5039c58bcb3e254aa1a35c1536d7eec.mimetex.gif) について、
について、![Tx = T\exp(At)T^{-1}Tx[0] = \exp(Jt)Tx[0]](./cache/05c778554753be3ae43630c097488470.mimetex.gif)
 の安定性と
の安定性と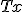 の安定性は一致する。
の安定性は一致する。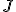 の固有値の実部が全て負ならば、
の固有値の実部が全て負ならば、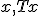 は原点に漸近安定。
は原点に漸近安定。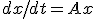 について、
について、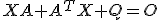 となる正定値行列
となる正定値行列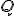 と対称行列
と対称行列 について、
について、 が漸近安定であることと
が漸近安定であることと が正定値であることは同値。
が正定値であることは同値。 が一意であることは講義では証明略。
が一意であることは講義では証明略。 として
として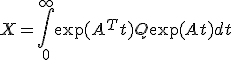 を選ぶと、正値対称。
を選ぶと、正値対称。![[\exp(A^T t)Q\exp(At)]_0^{\infty} = \int_0^{\infty}(d/dt)\exp(A^T t)Q\exp(At)dt = A^T X+XA](./cache/fba5b8711acb7a94442ab4261ab0b023.mimetex.gif)
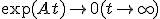 ならば、左辺は
ならば、左辺は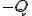 になるから、
になるから、 は
は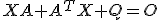 の正値対称な解になっている。
の正値対称な解になっている。 が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを
が、実部が非負の固有値を持つなら、その固有値・固有ベクトルを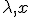 として、
として、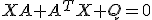 から、
から、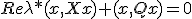 だが、各項が正なので、
だが、各項が正なので、 には実部が非負の固有値は存在しない。
には実部が非負の固有値は存在しない。
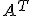 は
は の転置
の転置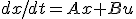
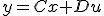
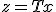 と変数変換すると、各係数は
と変数変換すると、各係数は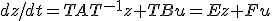
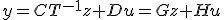
 をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに
をジョルダン標準形に直すと、状態方程式をジョルダンブロックごとに