![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
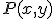 に対して、
に対して、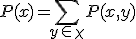 :
: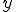 を指定しないときの
を指定しないときの の分布
の分布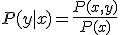 :特定の
:特定の が実現したと分かったときの
が実現したと分かったときの の分布
の分布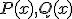 に対して、
に対して、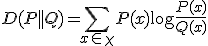
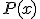 に対して、
に対して、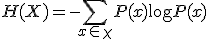
 のどれかが実現したときに得られる情報量の平均値。
のどれかが実現したときに得られる情報量の平均値。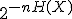 くらい
くらい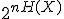 ほど。
ほど。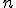 は系列の長さ。
は系列の長さ。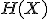 は各文字の出現確率のエントロピー。
対数の底は2をとっている。
は各文字の出現確率のエントロピー。
対数の底は2をとっている。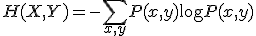
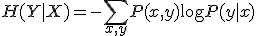
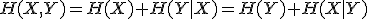
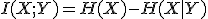 、
、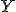 を知ることで
を知ることで について得られる情報量。
について得られる情報量。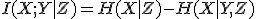 、
、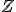 を知った上で
を知った上で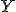 を知ったときに、
を知ったときに、 について得られる情報量。
について得られる情報量。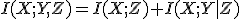
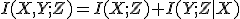
Presented by yambi. tzik all blame reserved.
面倒かもしれませんが,ミスは指摘してくださると助かります.
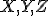 に対して,
に対して,
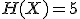 bits,
bits,
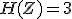 bits,
bits,
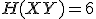 bits,
bits,
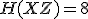 bits,
bits,
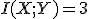 bits
の関係がある.
bits
の関係がある.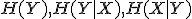 の値は?
の値は?
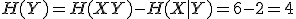
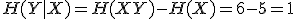
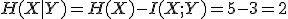
 と
と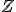 ,
,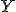 と
と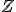 それぞれに関して,
次のどれが成立するか理由をつけて述べよ.
それぞれに関して,
次のどれが成立するか理由をつけて述べよ.
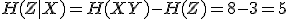 より,
より,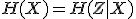 なので,
なので,
 と
と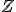 は確率的に独立.
は確率的に独立.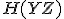 を求める方法がないので
を求める方法がないので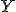 と
と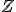 の独立性は判定不能.(私には判定できないでも可,なのかな.)
の独立性は判定不能.(私には判定できないでも可,なのかな.) のアルファベットのサイズは20より大きいか?
のアルファベットのサイズは20より大きいか?
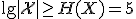 より,
より,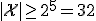 なので,20より大きい.
なので,20より大きい.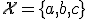 上の値をとる定常な単純マルコフ過程の遷移確率が次のように与えられている.
上の値をとる定常な単純マルコフ過程の遷移確率が次のように与えられている.
現状態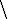 次状態 次状態 | a | b | c |
| a | 0.5 | 0.5 | 0 |
| b | 0.4 | 0 | 0.6 |
| c | 0.4 | 0.6 | 0 |
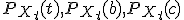 を求めよ.
を求めよ.
 と書くことにする.
と書くことにする.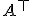 の固有値1に対応する固有ベクトルは
の固有値1に対応する固有ベクトルは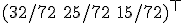 なので,
なので,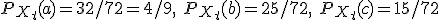 である.
である.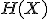 を,関数
を,関数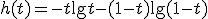 を用いて表せ.
を用いて表せ.
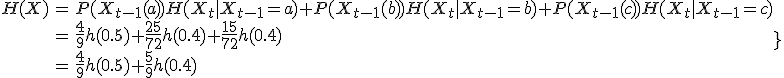
 と
と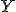 を歪を許して情報源符号化する場合を考える.
を歪を許して情報源符号化する場合を考える.
 と
と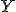 が共に2値で,その生起確率が
が共に2値で,その生起確率が
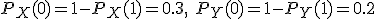 で与えられているものとする.
歪をハミング歪で測るものとして,
で与えられているものとする.
歪をハミング歪で測るものとして,
 を平均歪み
を平均歪み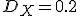 まで許して符号化する場合と
まで許して符号化する場合と
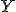 を平均歪み
を平均歪み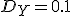 まで許して符号化する場合について考える.
最適な符号化が行える場合,どちらの方がより多くの符号化レートを必要とするか?
まで許して符号化する場合について考える.
最適な符号化が行える場合,どちらの方がより多くの符号化レートを必要とするか?
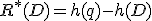 で与えられる(
で与えられる(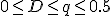 ).
).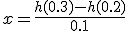 ,
,
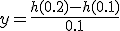 とおくと
とおくと
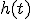 は凹関数なので
は凹関数なので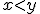 .
.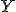 の方がより多くの符号化レートを必要とする.
の方がより多くの符号化レートを必要とする. と
と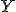 が,それぞれの分散
が,それぞれの分散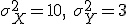 を持つ正規分布に従うものとする.
歪みを2乗誤差歪みで測るものとして,
を持つ正規分布に従うものとする.
歪みを2乗誤差歪みで測るものとして, を平均歪
を平均歪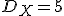 まで許して符号化する場合と,
まで許して符号化する場合と,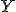 を平均歪み
を平均歪み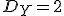 までえ許して符合化する場合を考える.最適な符号化が行える場合,どちらのほうがより多くの符号化レートを必要とするか?
までえ許して符合化する場合を考える.最適な符号化が行える場合,どちらのほうがより多くの符号化レートを必要とするか?
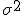 の正規分布における2乗誤差歪の符号化レートは
の正規分布における2乗誤差歪の符号化レートは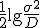 で与えられる.
で与えられる. の符号化レートは
の符号化レートは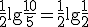 ,
,
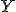 の符号化レートは
の符号化レートは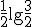 なので,
なので,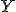 より多くの符号化レートを必要とする.
より多くの符号化レートを必要とする.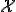 と出力アルファベット
と出力アルファベット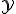 が
が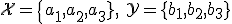 であるとする.
このとき,通信路の遷移確率
であるとする.
このとき,通信路の遷移確率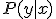 次のように与えられる時,
それぞれの通信路容量
次のように与えられる時,
それぞれの通信路容量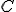 を関数
を関数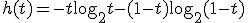 を用いて表せ.
を用いて表せ.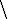 | 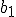 | 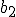 | 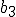 |
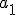 | 0.8 | 0.2 | 0 |
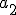 | 0 | 0.8 | 0.2 |
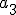 | 0.2 | 0 | 0.8 |
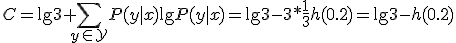
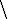 | 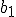 | 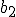 | 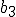 |
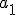 | 0.3 | 0 | 0.7 |
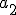 | 0 | 1 | 0 |
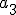 | 0.7 | 0 | 0.3 |
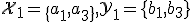 からなる通信路
からなる通信路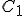 と
と
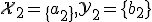 からなる通信路
からなる通信路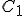 と
の和通信路なので,
と
の和通信路なので,
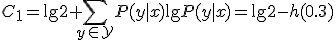
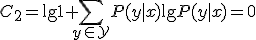
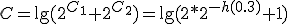
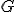 が次式で与えられるハミング符号がある.
が次式で与えられるハミング符号がある.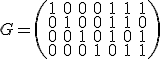
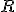 を求めよ.
を求めよ.
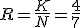
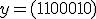 を受信した時,そのシンドロームを求め,
この
を受信した時,そのシンドロームを求め,
この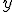 に誤りが含まれているか否かを定めよ.
誤りがない場合は「誤りなし」と下記,その理由を説明せよ.
また,誤りが含まれている場合は,1ビットの誤りであると仮定してその誤りを訂正せよ.
に誤りが含まれているか否かを定めよ.
誤りがない場合は「誤りなし」と下記,その理由を説明せよ.
また,誤りが含まれている場合は,1ビットの誤りであると仮定してその誤りを訂正せよ.
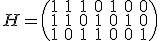
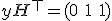
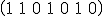
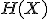 ,微分エントロピー
,微分エントロピー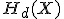 ,
相互情報量
,
相互情報量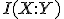 ,相対エントロピー
,相対エントロピー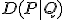 などの情報量は全て非負の量である.
などの情報量は全て非負の量である.
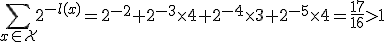
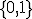 を100ビット用いると
を100ビット用いると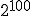 の情報を表現できる.
しかし,通信路容量
の情報を表現できる.
しかし,通信路容量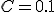 を持つ2値対称通信路を通して情報を伝送する場合は,誤りが生じる可能性がある.
誤り訂正するためには
を持つ2値対称通信路を通して情報を伝送する場合は,誤りが生じる可能性がある.
誤り訂正するためには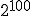 個全てを符号語として用いることができず,
冗長性を持たせてその一部のみ符号語として用いることになる.
通信路容量
個全てを符号語として用いることができず,
冗長性を持たせてその一部のみ符号語として用いることになる.
通信路容量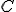 が0.1なので,十分余裕を見て
が0.1なので,十分余裕を見て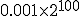 個程度の符号後を,ハミング距離が互いにもっとも離れるように配置すれば,十分小さい復号誤り率を達成できる誤り訂正符号が作れる.
個程度の符号後を,ハミング距離が互いにもっとも離れるように配置すれば,十分小さい復号誤り率を達成できる誤り訂正符号が作れる.
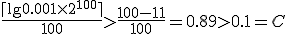 なので通信路符号化定理の強逆定理より復号誤り率は符号語長を長くすると1に近づいてしまう.
なので通信路符号化定理の強逆定理より復号誤り率は符号語長を長くすると1に近づいてしまう.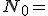 (Watt/Hz)を持つ
加法的白色ガウス雑音通信路に対して,時間連続信号波形
(Watt/Hz)を持つ
加法的白色ガウス雑音通信路に対して,時間連続信号波形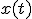 を用いて情報を伝送する場合を考える.
を用いて情報を伝送する場合を考える.
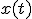 を用いて最大で
を用いて最大で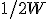 秒ごとに独立な情報を送ることができる.
したがって,信号電力
秒ごとに独立な情報を送ることができる.
したがって,信号電力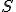 が一定の時,帯域幅
が一定の時,帯域幅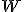 を
大きくすれば送れる情報量が増え,その通信路容量
を
大きくすれば送れる情報量が増え,その通信路容量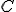 も
も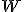 の増加につれていくらでも大きくできる.
の増加につれていくらでも大きくできる.
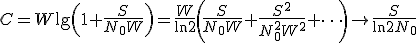
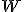 を増加させても
を増加させても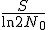 に収束してしまう.
に収束してしまう.