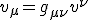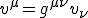講義日程-2007年度冬学期
幾何数理工学 †
- 担当:増田 直紀 講師
- 1.5単位
- 8:30-10:00 工学部六号館 62講義室
- レポート1~2回、中間試験、期末試験
内容 †
- 幾何学(Geometry)
様々な図形を一定の視点の下で眺め、これらの図形の性質を研究。
一定の視点とは、何らかの変換。図形の性質とは、その変換で不変な性質。
- 位相幾何学(Topology):位相同型変換によって不変な位相空間の性質を扱う。
- テンソルの幾何学:座標変換(C^∞級同型)によって不変な多様体の性質?
- トポロジー
- ユークリッド幾何学(Euclidean Geometry)
合同変換(Congrument Transformation)によって不変な図形の幾何学。
合同変換:二点間の距離を変えない変換。(平行移動・回転・鏡映とその合成)
長さ・角度・面積などが不変量。
- 位相幾何学(Topological Geometry)
位相同型写像で
位相同型写像:連続な全単射で逆写像も同型なもの。
長さ・角度・面積などは変化する。
図形のつながり方が不変。図形に空いた穴や図形のねじれ、境界の開・閉。
伸縮させて同じ形にできる図形は同じものとみなす。
コーヒーカップとドーナツは位相同型。
- 距離空間(Metric Space):距離関数の備わった集合。
- 距離関数:三角不等式を満たす、非負で対称な二変数関数で、密着でないもの。
- 距離空間X,Yについて、
{a[n]}_{n∈N}
lim[x→∞]a[n]=a
⇔(∀ε>0.∃n∈N.∀m>n⇒d(a[m],a)<ε)で極限を定義し、
f:X→Yについて、Xの任意の収束列{x[n]}について
lim[n→∞]f(x[n])=f(lim[n→∞]x[n])ならばfは連続と定義する。
∀ε>0.∃δ>0. ∀x,y∈X. d(x,y)<δ⇒d(f(x),f(y))<ε
∀x∈X.∀ε>0.∃δ>0. f(N(x,δ))⊂N(f(x),ε)
も同値。
- 連続でない写像で図形を変換すると、片方の空間で収束するものがもう片方では収束しない場合がある。
図形が破れている。
- 単射でない写像を使うと、異なる二点を同じ点に移すので、図形を張り合わせてしまっている。
- 逆写像が連続でない全単射では、境界の開の部分と閉の部分を張り合わせる場合が残っている。
- 位相空間(Topological Space):位相の備わった集合。距離空間の一般化。
- 位相:連続写像や極限を定義するための仕組み。
- 開集合系:有限積と加算和について閉じた集合族。
この集合族に属する集合を「開集合」とみなし、開集合の逆像が開集合になるような写像が連続写像。
- 閉集合系:有限和と加算積について閉じた集合族。
開集合系と同様に位相を定める。
- 近傍系:
- 閉包作用素:部分集合から部分集合への写像で、空を空に移し、合併とついて分配でき、冪等で拡大なもの。
- 位相同型写像:連続な全単射で逆写像も連続なもの。
「切り取らず」(連続)
貼り付けず(単射)、変形を許す写像(全射)。
- 距離空間の位相
- 距離空間X中の部分集合Aの点xについて、
Xに含まれるx周りの開球が存在すれば、xはAの内点。
存在しなければxはAの外点。
Aの外点全体を∂Aと書き、∂AをAの境界と呼ぶ。
(多様体の境界とは別物。)
- 開集合・閉集合の定義、その1
- 境界と交わりの無い集合が開集合。
- 境界を含む集合が閉集合。
- 開集合の補集合は閉集合。
閉集合の補集合は開集合。
空間と全体は開かつ閉な集合。
開でも閉でも無い集合もある。
- 開集合・閉集合の定義、その2
距離空間Xの部分集合Aについて
- A中の任意の点について、その点まわりの開球が存在すれば、Aは開集合。
- Aの補集合が開集合ならAは閉集合。
- この二種類の定義は同値だが、後者の方が位相空間に一般化しやすい。
- この開集合・閉集合の定義は距離に依存する。
例えば離散距離を入れれば任意のの部分集合は開かつ閉になる。
- 連続写像
- 距離空間X,Yとf:X→Yについて、次の3つは同値
- fが連続(⇔∀x∈X.∀U∈N(f(x))).∃V∈N(x). s.t. f(V)⊂U)
- Yの任意の開集合の逆像はXの開集合。
連続写像は開写像とは限らない。開を開へ移すとは限らない。
- Yの任意の閉集合の逆像はXの閉集合。
- 開集合・閉集合を距離に依存しない形で定義してやれば、
距離に依存せずに写像の連続性を定義できる。
- 「f:X→Yが位相同型写像」⇔「fは全単射で連続な開写像」
- 開集合の公理
- 距離空間Xの開集合全体をOとすると、Oは以下の開集合の公理を満たす。
- φ∈O, X∈O
- U,V∈O ⇒ U∩V∈O
(二つについて言えば再帰的に有限個について言った事になる)
∀x∈U∩V⇒∃α>0.∃β>0.N(x,α)⊂U∧N(x,β)⊂V⇒N(x,min(α,β))⊂U∩V
- {O[i]}_(i∈I). O[i]∈O. について、∪[i∈I]O[i] ∈ O
(Iの濃度については言及していない。任意の濃度でよい)
∀x∈∪[i∈I]O[i].∃i∈I.x∈O[i]⇒∃ε>0.N(x,ε)⊂O[i]⊂∪[i∈I]O[i]
- 閉集合の公理
- 距離空間Xの閉集合全体をFとすると、Fは以下の閉集合の公理を満たす。
- φ∈F, X∈F
- U,V∈F ⇒ U∪V∈F
- {O[i]}_(i∈I). O[i]∈O. について、∩[i∈I]O[i] ∈ O
- 補)集合論から
- 任意の集合Aについて、その部分集合全体は集合を成すと見なし、それを2^Aと表す。(冪集合の公理)
- 集合A,Bについて、AからBへの写像全体は集合を成し、B^Aと書く。
2={0,1}と見ると、冪集合2^AはAから2への写像全体と同型。
- 位相空間
必ずしも距離の入っていない集合について、開集合の公理を満たすように人工的に開集合を指定する。
- 開集合による位相
- 集合Xについて、開集合の公理を満たすXの部分集合族Tを、開集合系によるXの位相と呼び、位相を伴った集合(X,T)を位相空間と呼ぶ。
毎回ペアで書くのは面倒なので、どの位相を入れているか明らかなときにはTは省略されることが多い。
Tは一意には定まらない。位相の入れ方は複数考えられる。
位相には包含関係による順序づけができる。
開集合系による位相の定義以外にも閉集合系・近傍系・閉包作用素・開核作用素などでも位相を定義できる。
どれが一つで定義すればそこからほかのも定義できる。
- 位相空間(X,T)について、開集合系に含まれる集合を開集合。開集合の補集合を閉集合と呼ぶ。
- 最も弱い位相として密着位相{φ,X},最も強い位相として離散位相2^Xがある。
- 連続写像
- 位相空間 X,Y 間の写像 f:X→Y について、
fが連続であるとは、Yの任意の開集合の逆像がXの開集合であること。
- fが開写像であるとは、任意のXの開集合の像がYの開集合であること。
- 位相同型写像
- 位相空間の間の連続で全単射な開写像を位相同型写像・同相写像であるという。
- 二つの位相空間の間に位相同型写像が存在するとき、その位相空間は互いに同相であるという。
- 近傍系
- 位相空間X上の点xについて、xを含む開集合を開近傍。xの開近傍を含む集合を近傍と呼び、その全体をN(x)と表す。
- 「xを内点のとして含む集合」や「開核がxを含む集合」としても同値。
- AがXの開集合であることと、A上の任意の点についてAに含まれる近傍が存在することは同値。
- AがXの閉集合であることと、A^C上の任意の点についてAと交わらない近傍が存在することは同値。
- 位相空間X,Yについて、f:X→YがX上の点xにおいて連続であるとは、Yにおけるf(x)の任意の近傍Vについて、f(U)⊂Vとなるxの近傍Uが存在すること。
fがX上の任意の点で連続ならば、fはX全体で連続。
- 距離空間と位相空間
- 距離空間は距離に伴う通常の開集合系を使って位相を定められる。
特に(R^n,d_2)の位相をEuclid位相と呼ぶ。
- 連結性
- 開かつ閉な集合が全体と空集合以外になければ連結。
- 空でない互いに疎な開集合で全空間を分割できるなら不連結。
- コンパクト性
- ある集合族で集合を覆えるとき、その集合族を被覆という。
- 被覆に含まれる集合が全部開集合なら開被覆という。
- 開被覆の要素の数が有限なら有限開被覆という。
- 要素数を指定しない任意の開被覆から、有限開被覆を選び出せるとき、その集合はコンパクトだという。
- ユークリッド空間については、コンパクトであることと有界閉集合であることは同値。
- 直和分割
- 全空間を互いに疎な集合族に分割すること。
- 同値関係で同値類を作ると、同値類全部を集めたものは直和分割。
同値類による分割を分類と呼び、同値類全体の集合を商集合と呼ぶ。
集合の要素から、その要素が属する同値類への写像を標準全射と呼ぶ。
- 路,道,弧,パス
- 位相空間
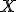 と任意の2点
と任意の2点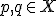 に対して、
に対して、
連続写像![f:[0,1]\to X](./cache/88b85fbd9cd7c1be650daf613bd6ab08.mimetex.gif) で
で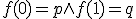 となるものをpからqへの路という。
となるものをpからqへの路という。
- 弧状連結
- 空間上の任意の2点について、それらを結ぶ路が存在すること。
- 弧状連結ならば連結。
- 路の変形,ホモトープ,ホモトピー
- 位相空間
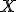 上の2点
上の2点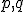 と
と
それらを結ぶ2つの路![f,g : [0,1]\to X](./cache/2e6d132f2126f51e4595ce3bd5a20a9d.mimetex.gif) について、
について、
「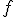 が
が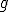 に変形できる」とは、
に変形できる」とは、
連続写像![F:[0,1]\times [0,1] \to X](./cache/d08fb0daf6267de7ce61c361a1b048b9.mimetex.gif) で、
で、
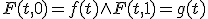 が存在するとき、
が存在するとき、
fはgに変形できる、と言い、Fはfからgへのホモトピーと呼び、
fとgは互いにホモトープと言う。
ホモトープであることは同値関係。
(空間上の2点を固定して)空間上の曲線をホモトープによる同値関係で分類できる。
- ホモトープによる同値類の数は位相不変量(同相写像によって変わらない性質。)
この商集合は有限集合になるとは限らず、扱いが難しい。
商集合に適当な演算を定義して群を作り、代数的な構造から元の空間の性質を調べる。
- 基本群
- 位相空間X上に基点pを決めたとき、基本群
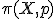 は
は
pを通る連続閉曲線をホモトープによる同値関係で割ったもの。
- 単体
位相空間上のm単体は、空間上の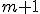 点を相互に交わらない曲線で結んだもの。
点を相互に交わらない曲線で結んだもの。
単体の辺は、m単体を構成する点から、任意にm個点を選んで作られた(m-1)単体。
点・線分・三角形・正四面体など、図形を構成するための基本図形。
- 複体
有限個の単体の集合 が複体であるとは、
が複体であるとは、
 に含まれる任意の単体の任意の辺が
に含まれる任意の単体の任意の辺が に含まれ、
に含まれ、
 に含まれる任意の2つの単体の共通部分は、空であるか
に含まれる任意の2つの単体の共通部分は、空であるか にふくまれること。
にふくまれること。
異なる複数の複体が同一の図形を表すこともある。
図形を単体に分割する方法は一つには決まらない。
- 単体写像
複体Kから複体Lへの写像で、Kに含まれる単体を
Lに含まれる単体に移す写像を単体写像と呼ぶ。
特に全単射な単体写像を単体同型写像と呼び、
単体同型写像が存在する2つの複体は、単体同型であるという。
単体同型な複体が表す多面体は、互いに位相同型になる。
- 細分
多面体として等しい2つの複体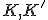 で、
で、
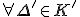 に対して
に対して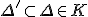 となるとき、
となるとき、
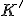 は
は の細分であるという。
の細分であるという。
- 組み合わせ同型
2つの複体に、それぞれの細分に単体同型となるものがあれば
その2つの単体は組み合わせ同型と呼ばれる。
- 記法
- 位相同型、
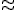 、位相空間同士に連続で開写像な全単射がある。
、位相空間同士に連続で開写像な全単射がある。
- 同値、
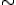 、反射律・対称律・推移律を満たす2項関係。
、反射律・対称律・推移律を満たす2項関係。
- ホモトープ同値、
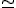 、位相空間上の曲線が連続的に移り変われること。
、位相空間上の曲線が連続的に移り変われること。
- 群の同型、
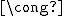 、群同士に群演算と両立する全単射があること。
、群同士に群演算と両立する全単射があること。
- 単体同型、
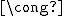 、複体同士に構造を保つ全単射があること。
、複体同士に構造を保つ全単射があること。
- 組み合わせ同型、
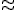 、複体同士が、単体同型な細分を持つこと。
、複体同士が、単体同型な細分を持つこと。
- 組み合わせ的にホモトープ、
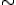 、折れ線同士が初等変形で移り変われる。
、折れ線同士が初等変形で移り変われる。
基本群を定義から直接求めて、同型かどうかを調べるのは難しい、
位相空間に複体構造を入れて、折れ線群を定義できると、計算が容易になる。
- 複体上の折れ線
複体上の1単体を連ねたものを、複体上の折れ線と呼ぶ。
- 折れ線の積
複体 上の2つの折れ線
上の2つの折れ線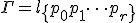
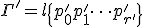 で、
で、
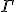 の終点
の終点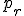 と
と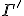 の始点
の始点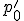 が一致するとき、
が一致するとき、
2つの折れ線に積が定義でき、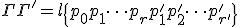
と、折れ線を繋いだものを積とする。
- 折れ線の初等変形
以下の操作とその逆を折れ線の初等変形という。
- 同じ点が2つ続いたら、1つを除くこと。
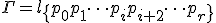
- 同じ点に挟まれた点を除くこと、
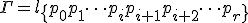
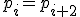
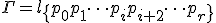
- 連続する3つの点からなる単体がもとの複体に含まれるとき、
中間の点を除くこと。
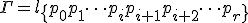
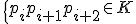
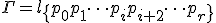
- 組み合わせ的にホモトープ、折れ線同値
始点と終点が一致する二つの折れ線が、初等変形で移り変われるとき、
その2つの折れ線は組み合わせ的にホモトープという。
- 折れ線群
複体上に基点を1つ選び、その点を通る閉折れ線を
組み合わせホモトピーの同値関係で割ったものは
折れ線の連結について群になり、それを複体上の折れ線群と呼ぶ。
複体の折れ線群と、複体が構成する多面体の基本群は群として同型。
- ホモロジー
閉曲線による切断に注目する。
例えばトーラスをループで切断するとき、
トーラスを二つの部分に分割するループと
分割しないループがある。
球面上でなら、どのループで切断しても二つの部分に分かれる。
- 単体の向き
多角形として同じ単体が同じ向きであるとは、単体をなす点の列が互いに偶置換で移り変われること。
逆向きであるとは、奇置換で移り変われること。
- 凖同型定理
2つの群の間の凖同型写像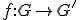 について、
について、
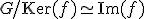
- ホモロジー群
- 複体
 の
の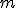 次元サイクル:
次元サイクル: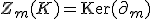
- 複体
 の
の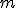 次元境界サイクル:
次元境界サイクル: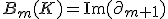
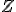 は切断を表す
は切断を表す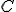 の部分群。
の部分群。
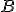 は図形を分ける切断を表す
は図形を分ける切断を表す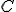 の部分群。
の部分群。
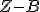 が図形を分けない切断を表している。
が図形を分けない切断を表している。
境界サイクル分の違いを無視して、
ホモロジー群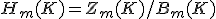 を作れば複体の穴の状態を反映した群ができあがる。
を作れば複体の穴の状態を反映した群ができあがる。
- ホモローグ
2つの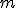 次元サイクル
次元サイクル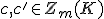 がホモローグであるとは、
がホモローグであるとは、
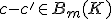 であること。
であること。
ホモローグは同値関係。ホモローグによる同値類はホモロジー類と呼ばれる。
- 来週は中間テスト。持ち込み可。折れ線まで。印刷物は50枚まで。
- 複体
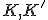 について、
について、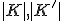 が位相同型ならば、
が位相同型ならば、
そのホモロジー群も同型。
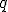 次元ホモロジー群は有限生成な可換群なので、
次元ホモロジー群は有限生成な可換群なので、
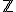 と
と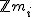 の有限な直和で一意に表される。
の有限な直和で一意に表される。
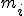 は
は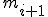 の約数になっている。
の約数になっている。
ここに現れる無限巡回群の個数を、 の
の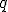 次元ベッチ数といい、
次元ベッチ数といい、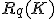 と書く。
と書く。
有限巡回群の列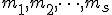 を
を の
の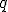 次元ねじれ係数という。
次元ねじれ係数という。
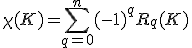 をオイラー標数と呼ぶ。
をオイラー標数と呼ぶ。
- オイラー・ポアンカレの定理
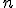 次元複体
次元複体 に含まれる
に含まれる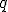 次元単体の個数を
次元単体の個数を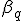 とすると、
とすると、
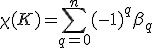 が成立。
が成立。
- テンソル
スカラー・ベクトル・行列と直交座標・直交変換では、応用上不十分なこともある。
テンソルはそれらの一般化。
量同士の関係を座標変換に対して不変な形で書くための道具。
- 線型空間とその双対空間
線型空間上の連続な線型関数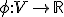 を
を
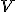 の線型汎関数という。
の線型汎関数という。
和とスカラー倍を関数値の和とスカラー倍で定義すれば、
線型汎関数全体は線型空間になっている。
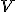 上の線型汎関数のつくる線型空間を
上の線型汎関数のつくる線型空間を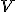 の双対空間と呼び、
の双対空間と呼び、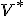 と書く。
と書く。
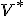 の双対空間
の双対空間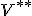 は(有限次元なら)もとの空間
は(有限次元なら)もとの空間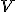 と一致する。
と一致する。
もとのベクトル空間の基底は下付き添字を使って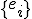 で書き、
で書き、
その双対基底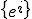 、
、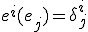 は上付き添字で書く。
は上付き添字で書く。
- 反変ベクトルと共変ベクトル
ベクトル空間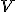 での2つの基底
での2つの基底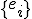
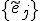 の間の基底の変換に対して、
の間の基底の変換に対して、
ベクトルの成分の変換は、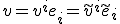
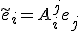
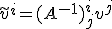 となる。
となる。
この変換のされ方をする2つの量は、互いに反変的であるといい、
基底に対して反変的なベクトルを反変ベクトル(contravariant vector,vector)と言う。
対して、双対空間のベクトルの基底と成分は、
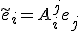
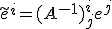
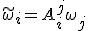
この変換のされ方をする2つの量は、互いに共変的であるといい、
もとの線形空間の基底に対して共変的なベクトルを共変ベクトル(covariant vector,covector)と言う。
- 例
- 座標の微分は反変ベクトル。アフィン空間なら座標の差は反変ベクトル。
- スカラー関数のgradは共変ベクトル。アフィン空間なら共変p階,反変q階のテンソルの偏微分は共変(p+1)階,反変q階のテンソル。
- 共変p階,反変q階のテンソルの外微分は共変(p+1)階,反変q階のテンソル。
- 高階の共変テンソル
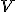 上の多重線形な連続汎関数
上の多重線形な連続汎関数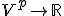 のなす線形空間を
のなす線形空間を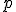 階の共変テンソル空間と呼び、
階の共変テンソル空間と呼び、
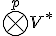 と書く。
と書く。
- 共変テンソルの演算
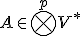 の元と
の元と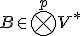 のテンソル積、
のテンソル積、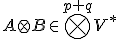 を、
を、
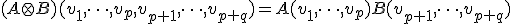 で定義する。
で定義する。
テンソル積は結合的で線形。
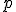 階の共変テンソルは反変基底に対する作用で特徴付けられる。
階の共変テンソルは反変基底に対する作用で特徴付けられる。
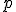 個の添字を持つ成分数
個の添字を持つ成分数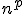 個の量の組。
個の量の組。
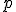 階共変テンソルの基底は双対基底の
階共変テンソルの基底は双対基底の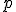 個の直積。
個の直積。
- 共変テンソルの座標変換
基底空間の座標変換に対して共変テンソルは、各添字について変換行列の逆行列がかかる形で変換される。
- 高階の反変テンソル
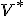 上の多重線形な連続汎関数
上の多重線形な連続汎関数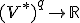 のなす線形空間を
のなす線形空間を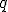 階の反変テンソルと呼び、
階の反変テンソルと呼び、
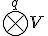 と書く。
と書く。
反変テンソルについても共変テンソルと同じようにいろいろ定義される。
- 混合テンソル
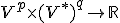
- 対称テンソル・交代(反対称)テンソル
対称性・交代性は座標変換に依らない性質。
- 高階テンソルの共変添字の組、反変添字の組について、
添字の任意の置換についてテンソル全体が不変であるとき、
そのテンソルはその添字の組について対称であるという。
テンソルを多重線形汎関数と見るなら、
特定の引数の組の置換についての不変性を指す。
- 同様に、添字の組の任意の奇置換について符号が入れ替わるとき
そのテンソルはその添字の組について交代であるという。
- 対称化作用素
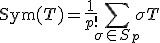
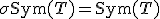
- 交代化作用素
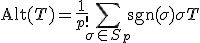
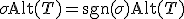
- 計量
内積を与える2階の対称共変テンソル。
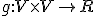
正値対称双線形な連続関数。
反変ベクトル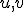 について、その内積を
について、その内積を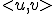 と書く。
と書く。
基底を定めれば、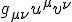
- ベクトルの長さ
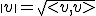
- ベクトルのなす角度
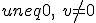 のなす角度は
のなす角度は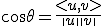 で定義する。
で定義する。
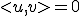 なら直交するという。
なら直交するという。
- 計量の入った線型空間を計量線型空間、Euclid空間と呼ぶ。
計量の無い空間では、長さや角度は定義できない。
平行・向きは定義できる。
- 直交座標系
正値対称な2階の共変テンソルは対角化可能。
底空間に適切な座標変換をすると、計量テンソルは(局所的には)単位行列にできる。
- 内積と双対空間
ベクトル空間に内積が与えられると、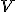 と
と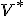 の間に
の間に
(座標系に依らない)標準的な変換が存在する。
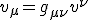
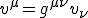
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
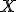 と任意の2点
と任意の2点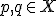 に対して、
に対して、![f:[0,1]\to X](./cache/88b85fbd9cd7c1be650daf613bd6ab08.mimetex.gif) で
で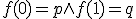 となるものをpからqへの路という。
となるものをpからqへの路という。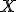 上の2点
上の2点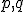 と
と![f,g : [0,1]\to X](./cache/2e6d132f2126f51e4595ce3bd5a20a9d.mimetex.gif) について、
について、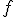 が
が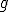 に変形できる」とは、
に変形できる」とは、![F:[0,1]\times [0,1] \to X](./cache/d08fb0daf6267de7ce61c361a1b048b9.mimetex.gif) で、
で、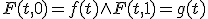 が存在するとき、
が存在するとき、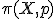 は
は 点を相互に交わらない曲線で結んだもの。
点を相互に交わらない曲線で結んだもの。 が複体であるとは、
が複体であるとは、 に含まれる任意の単体の任意の辺が
に含まれる任意の単体の任意の辺が に含まれ、
に含まれ、 に含まれる任意の2つの単体の共通部分は、空であるか
に含まれる任意の2つの単体の共通部分は、空であるか にふくまれること。
にふくまれること。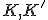 で、
で、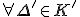 に対して
に対して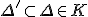 となるとき、
となるとき、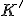 は
は の細分であるという。
の細分であるという。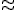 、位相空間同士に連続で開写像な全単射がある。
、位相空間同士に連続で開写像な全単射がある。 、反射律・対称律・推移律を満たす2項関係。
、反射律・対称律・推移律を満たす2項関係。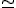 、位相空間上の曲線が連続的に移り変われること。
、位相空間上の曲線が連続的に移り変われること。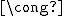 、群同士に群演算と両立する全単射があること。
、群同士に群演算と両立する全単射があること。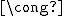 、複体同士に構造を保つ全単射があること。
、複体同士に構造を保つ全単射があること。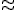 、複体同士が、単体同型な細分を持つこと。
、複体同士が、単体同型な細分を持つこと。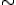 、折れ線同士が初等変形で移り変われる。
、折れ線同士が初等変形で移り変われる。 上の2つの折れ線
上の2つの折れ線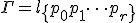
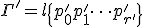 で、
で、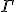 の終点
の終点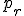 と
と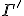 の始点
の始点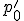 が一致するとき、
が一致するとき、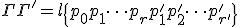
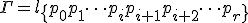
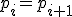
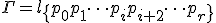
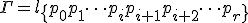
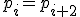
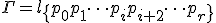
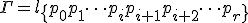
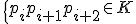
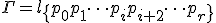
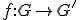 について、
について、
 の
の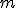 次元サイクル:
次元サイクル: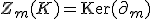
 の
の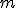 次元境界サイクル:
次元境界サイクル: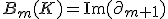
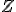 は切断を表す
は切断を表す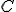 の部分群。
の部分群。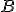 は図形を分ける切断を表す
は図形を分ける切断を表す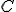 の部分群。
の部分群。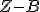 が図形を分けない切断を表している。
が図形を分けない切断を表している。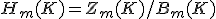 を作れば複体の穴の状態を反映した群ができあがる。
を作れば複体の穴の状態を反映した群ができあがる。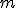 次元サイクル
次元サイクル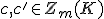 がホモローグであるとは、
がホモローグであるとは、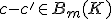 であること。
であること。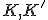 について、
について、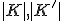 が位相同型ならば、
が位相同型ならば、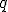 次元ホモロジー群は有限生成な可換群なので、
次元ホモロジー群は有限生成な可換群なので、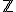 と
と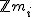 の有限な直和で一意に表される。
の有限な直和で一意に表される。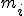 は
は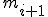 の約数になっている。
の約数になっている。 の
の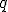 次元ベッチ数といい、
次元ベッチ数といい、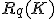 と書く。
と書く。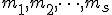 を
を の
の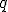 次元ねじれ係数という。
次元ねじれ係数という。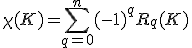 をオイラー標数と呼ぶ。
をオイラー標数と呼ぶ。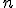 次元複体
次元複体 に含まれる
に含まれる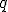 次元単体の個数を
次元単体の個数を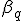 とすると、
とすると、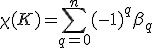 が成立。
が成立。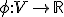 を
を の線型汎関数という。
の線型汎関数という。 上の線型汎関数のつくる線型空間を
上の線型汎関数のつくる線型空間を の双対空間と呼び、
の双対空間と呼び、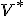 と書く。
と書く。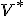 の双対空間
の双対空間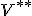 は(有限次元なら)もとの空間
は(有限次元なら)もとの空間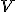 と一致する。
と一致する。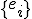 で書き、
で書き、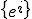 、
、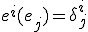 は上付き添字で書く。
は上付き添字で書く。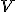 での2つの基底
での2つの基底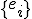
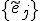 の間の基底の変換に対して、
の間の基底の変換に対して、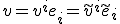
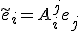
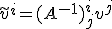 となる。
となる。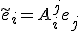
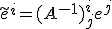
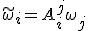
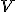 上の多重線形な連続汎関数
上の多重線形な連続汎関数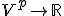 のなす線形空間を
のなす線形空間を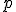 階の共変テンソル空間と呼び、
階の共変テンソル空間と呼び、 と書く。
と書く。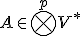 の元と
の元と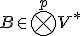 のテンソル積、
のテンソル積、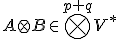 を、
を、
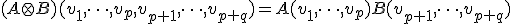 で定義する。
で定義する。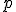 階の共変テンソルは反変基底に対する作用で特徴付けられる。
階の共変テンソルは反変基底に対する作用で特徴付けられる。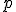 個の添字を持つ成分数
個の添字を持つ成分数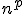 個の量の組。
個の量の組。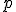 階共変テンソルの基底は双対基底の
階共変テンソルの基底は双対基底の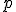 個の直積。
個の直積。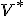 上の多重線形な連続汎関数
上の多重線形な連続汎関数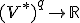 のなす線形空間を
のなす線形空間を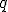 階の反変テンソルと呼び、
階の反変テンソルと呼び、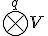 と書く。
と書く。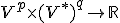
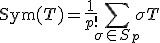
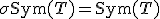
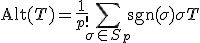
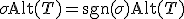
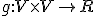
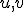 について、その内積を
について、その内積を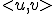 と書く。
と書く。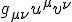
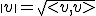
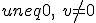 のなす角度は
のなす角度は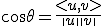 で定義する。
で定義する。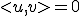 なら直交するという。
なら直交するという。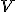 と
と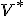 の間に
の間に